A Brief Summary of Proof Aggregation
Tomas Krnak

Intro
In the ever-evolving landscape of blockchain technology, ensuring privacy and scalability while maintaining security remains a paramount challenge. Succinct non-interactive arguments of knowledge (SNARKs) have emerged as a powerful cryptographic tool to address the scalability challenges, significantly reducing the storage and computational means required for blockchain validation. Additionally, the nature of SNARKs enables a sensitive parts of transactions to remain private, which opens door for more confidential and surveillance-resistant ledgers.
Proof [1] aggregation is a method where the prover collects several proofs and produces a new proof that proves the validity of the initial proofs. This concept has garnered significant attention among blockchain researchers in both the industry and academia. By aggregating multiple proofs into a single proof, it becomes possible to reduce the computational and storage overhead associated with verifying large batches of transactions or more generally any kind of computations. This not only enhances the efficiency of blockchain networks, but also opens up new possibilities for scaling decentralized applications and improving user privacy. However, generation of an aggregated proof costs extra computational resources, which, particularly for blockchain rollups, leads to delayed finality.
In this post, I summarize my research on proof aggregation tools and techniques introduced in the past few years. First, I discuss two algebraic aggregation methods for SNARKs based on inner product arguments. Then I move to recursive proof systems. It turns out that recursion on pairing-friendly elliptic curves always has some caveats and recursion on a 2-cycle of elliptic curves is usually not fully succinct. Finally, I leave elliptic curves cryptography, entering the realm hash-based recursive STARKs, which have become quite popular among rollups providers in past two years.
Throughout the post, I delve into the constraints of individual aggregation schemes and explore various trade-offs between aggregation efficiency, proof size, and verification time. Particularly, I focus on the hidden pitfalls of each construction. Uncovering these little concealed caveats may not be straightforward but is crucial for making an informed decision on the most suitable scheme for a specific application. For instance, a notable drawback of certain aggregation schemes is the inability to further aggregate proofs using the same scheme. Other caveats may include the requirement of a trusted setup or unexpectedly prolonged proof verification time. Lastly, I provide a comprehensive comparison of the properties of each aggregation scheme in a detailed table.
Individual sessions are illustrated with simplified sketches of discussed schemes. In these illustrations, I often denote provers by and proofs by
Aggregation via Inner Product Arguments
Widely used SNARKs like Groth16 (2016) and Plonk (2019) use pairing-friendly elliptic curves to achieve small proof size and low verification cost. In this section, I provide an overview of two aggregation methods that benefit from the bilinearity of pairings: SnarkPack for aggregation of Groth16 proofs and aPlonK for aggregation for PlonK proofs.
SnarkPack
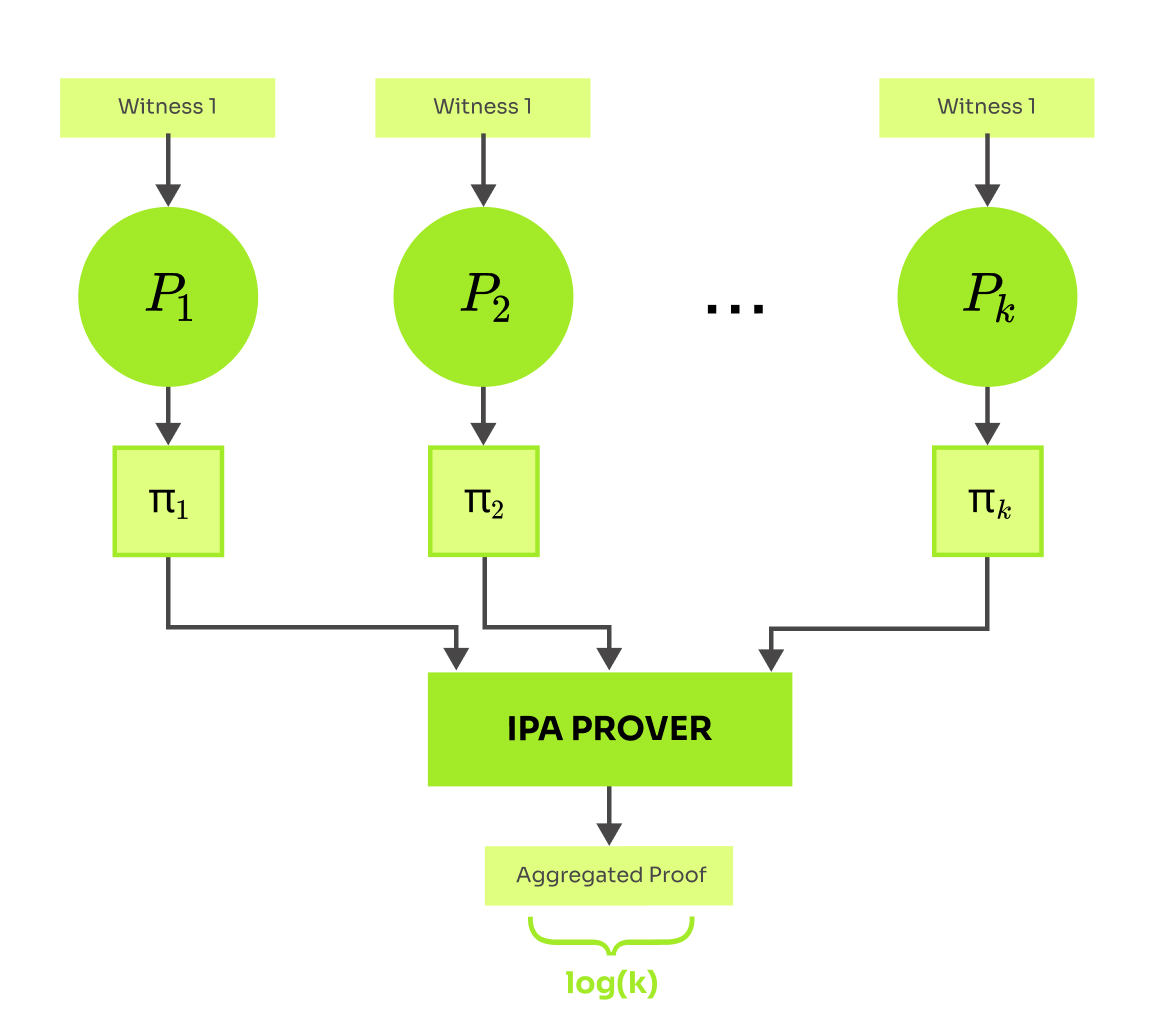
SnarkPack SnarkPack (2021) is an aggregation scheme for Groth16 proofs. One Groth16 proof consists of only 3 elliptic curve points and its verification requires checking the equality of this form
where denotes the pairing operation, is encoding of a public input and is some fixed EC point. Therefore verification of a batch of proofs and encoded public inputs means checking that
High-level idea of the SnarkPack is: First, pick a random scalar and squash all these checks into one by a random linear combination , getting a single equality
to be checked. Second, use techniques based on Inner Product Arguments (IPA) to delegate computation of the first and the last product in the equation to a prover.
This construction leads to log-sized proofs with logarithmic verification time relative to the number of aggregated proofs. The initiation of SnarkPack requires two trusted setups. Luckily, SnarkPack does not depend on any new special structure of the setup, and therefore the Zcash and Filecoin setups can be reused.
To give some concrete figures, “SnarkPack can aggregate 8192 proofs in 8.7s and verify them in 163ms”. Comparing SnarkPack proof with a raw batch of k Groth16 proofs, SnarkPack proof will become smaller for k≥128 and its verification is more efficient already for k≥32 proofs.
aPlonk
The Aggregated PlonK (2022) protocol extends the ideas of SnarkPack to PlonK. Unlike Groth16, the verification procedure of PlonK proofs is relatively complex, which brings a lot of new challenges and imposes limitations to their aggregation. One of the main limitations of aPlonK is that provers must run synchronously, sharing round challenges and the same circuit. However “our system [aPlonk] is perfectly applicable to creating a validity rollup”, the authors claim.
The aPlonK article introduces a new cryptographic primitive called multi-polynomial commitment scheme (MPCS), which is a useful abstraction for the techniques introduced in SnarkPack, offering a more modular framework conducive to future developments in the field. Furthermore, the authors noticed that weaker assumptions (inner-product binding and inner-product extractability) suffice for constructing MPCS, resulting in ~50% reduction in the size and verification time of the aggregated proof and ~50% smaller proving key. I believe that this enhancement is applicable to SnarkPack too.
Let’s compare an aPlonK proof with a batch of PlonK proofs. According to the article, “aPlonK becomes more efficient after a threshold of about 300 proofs” and “the proof size of aPlonK becomes smaller starting from 64 proofs”. Further, “we can see an overhead of approximately 20% (45 seconds) for aPlonK proving time for 4096 aggregated proofs. This represents 1% of the total machine time.” (2.9GHz Intel Xeon Platinum 8375C vCPU with 1 TB of RAM and 128 processors).
Aggregation via curves chains
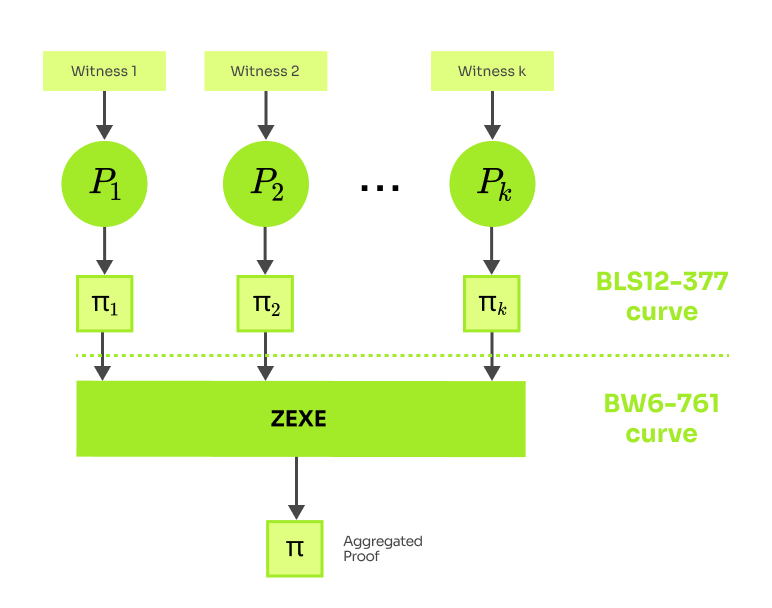
Before we enter the landscape of recursive SNARKs, I want to mention one more smart proof aggregation approach. The ZEXE (2018) scheme by Aleo uses a tailored Pinch-Cook curve BW6-761 to efficiently aggregate proofs over the BLS12-377 curve. We call this tuple of curves a 2-chain, because the base field of BLS12-377 is the scalar field of BW6-761. Unlike SnarkPack and aPlonK, ZEXE aggregated proofs have constant size and verification time. Notice though that similarly to these two schemes, ZEXE aggregated proofs cannot be further aggregated. For that purpose we would need a longer chain of curves.
The aggregation algorithm is simply the Groth16 SNARK over BW6-761 for a circuit verifying k proofs. Verification of one proof over BLS12-377 requires ~45k constraints. Notice that the base field of BW6-761 is ~2x larger than the base field of standard BLS12-377, therefore all arithmetic operations of the aggregation layer are 2-4x slower. The consequent work VERI-ZEXE (2022) replaces Groth16 by PlonK, gaining ~10x prover efficiency and ~21k constraints verifier gadget.
Intermezzo on proof aggregation via recursive SNARKs
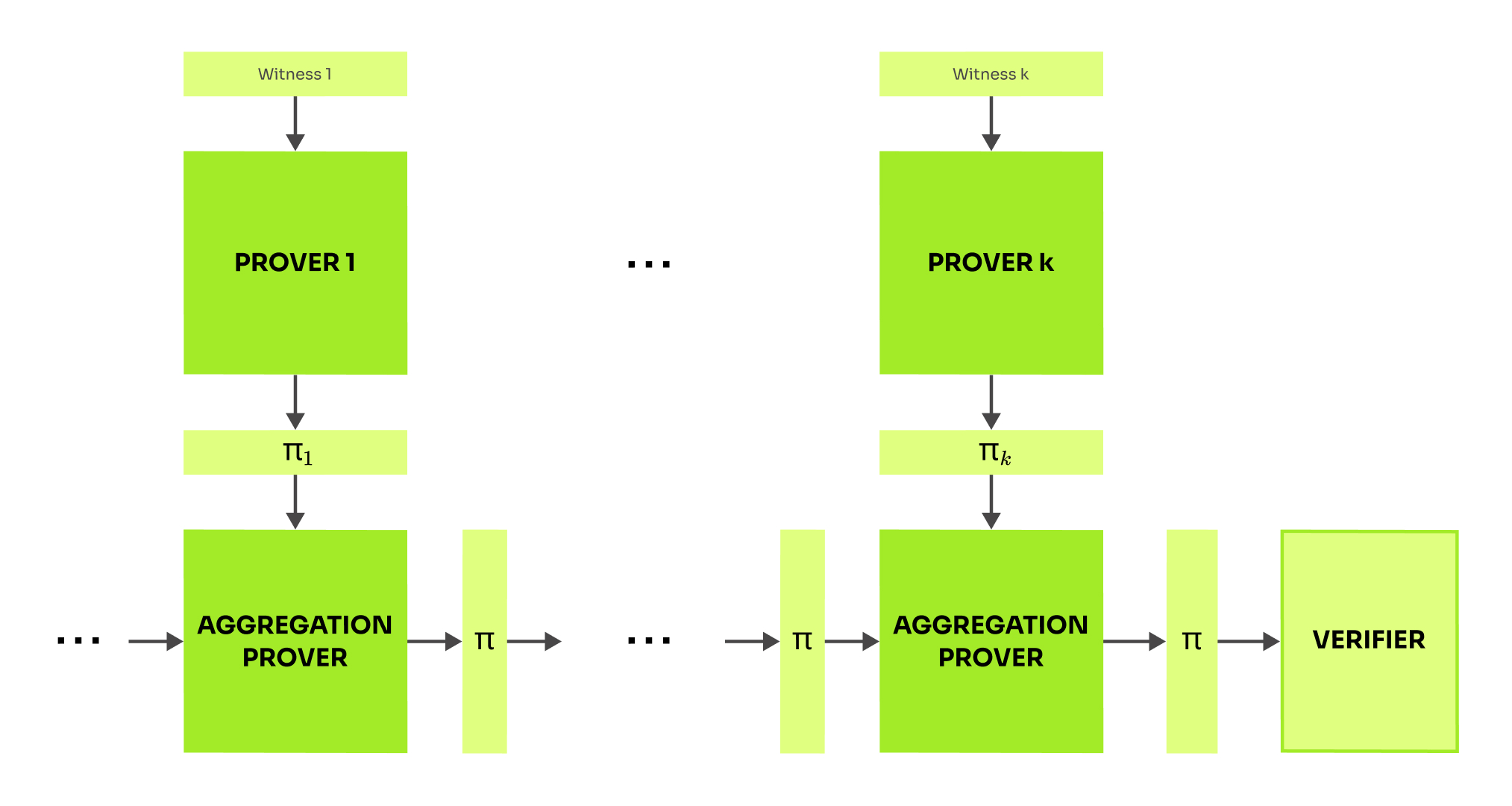
In the rest of the post we focus on recursive proof systems. We say that a SNARK is recursive, if it enables to efficiently prove claims about validity of its proofs. Let me explain how the recursion is related to the proof aggregation. Lets say that we have two transactions t1 and t2 attested by two proofs p1 and p2. A recursive SNARK allows us to generate a single proof for the claim “There exist valid proofs that prove the validity of t1 and t2.” We have just compressed proofs p1 and p2 into a single proof! Furthermore this procedure can be repeated and thus unlimited number of proofs can be aggregated into one.
Let's compare aggregation via recursion with the SnarkPack and aPlonK protocols outlined above. First, a notable advantage of recursion-based aggregation is its flexibility regarding the number of aggregated proofs, which doesn't need to be predetermined. This enables construction of succinct blockchains such as Mina (2020), where the proof of the validity of the last block attests validity of all previous blocks in a blockchain. Second, the size and verification time of the resulting aggregated proof remain independent of the number of proofs aggregated. Third, while SnarkPack and aPlonK execute algebraic manipulations on a batch of proofs, resulting in a relatively lightweight aggregation process, recursion introduces computation over a recursive circuit to produce a completely new proof, thereby consuming additional resources. The efficiency of recursion-based aggregation schemes is contingent upon the recursion threshold of an underlying SNARK. This threshold denotes the number of arithmetic gates needed to express the SNARK verifier as an arithmetic circuit.
How do Groth16 and PlonK fare in terms of recursion threshold? Unfortunately, it appears that representing a pairing operation within a SNARK circuit is exceedingly resource-intensive. Specifically, representation of one pairing operation translates into 24.7 millions (~2^25) constraints (R1CS), resulting in 15 GB proving key and 4.2 hours circuit compilation time (AWS r5.8xlarge instance, 32-core 3.1GHz, 256G RAM), according to this benchmark. Verification of Groth16 proofs requires computing 3 pairings and verification of PlonK proofs requires 2 pairings. These demanding requirements make naive recursion impractical for both Groth16 and PlonK.
This enormous number of constraints stems from the necessity of expressing non-native arithmetic [2] operations in the circuit. Some recursive SNARKs avoid non-native arithmetic by using 2-cycles of elliptic curves (instead of pairing-friendly curves) at the expense of larger proof size. Are there curves supporting both (2-cycles & pairings)? Yes, but unfortunately they are inefficient at 128-bit security level. Aztec protocol (2021) bypasses this by relying on efficient half-pairing cycle BN254/Grumpkin, where only BN254 supports pairings. The BN254 curve is currently used in Ethereum, even though its safety has been doubted and theoretically reaches only 103-bits against STNFS algorithm.
Pairing-enhanced PlonK
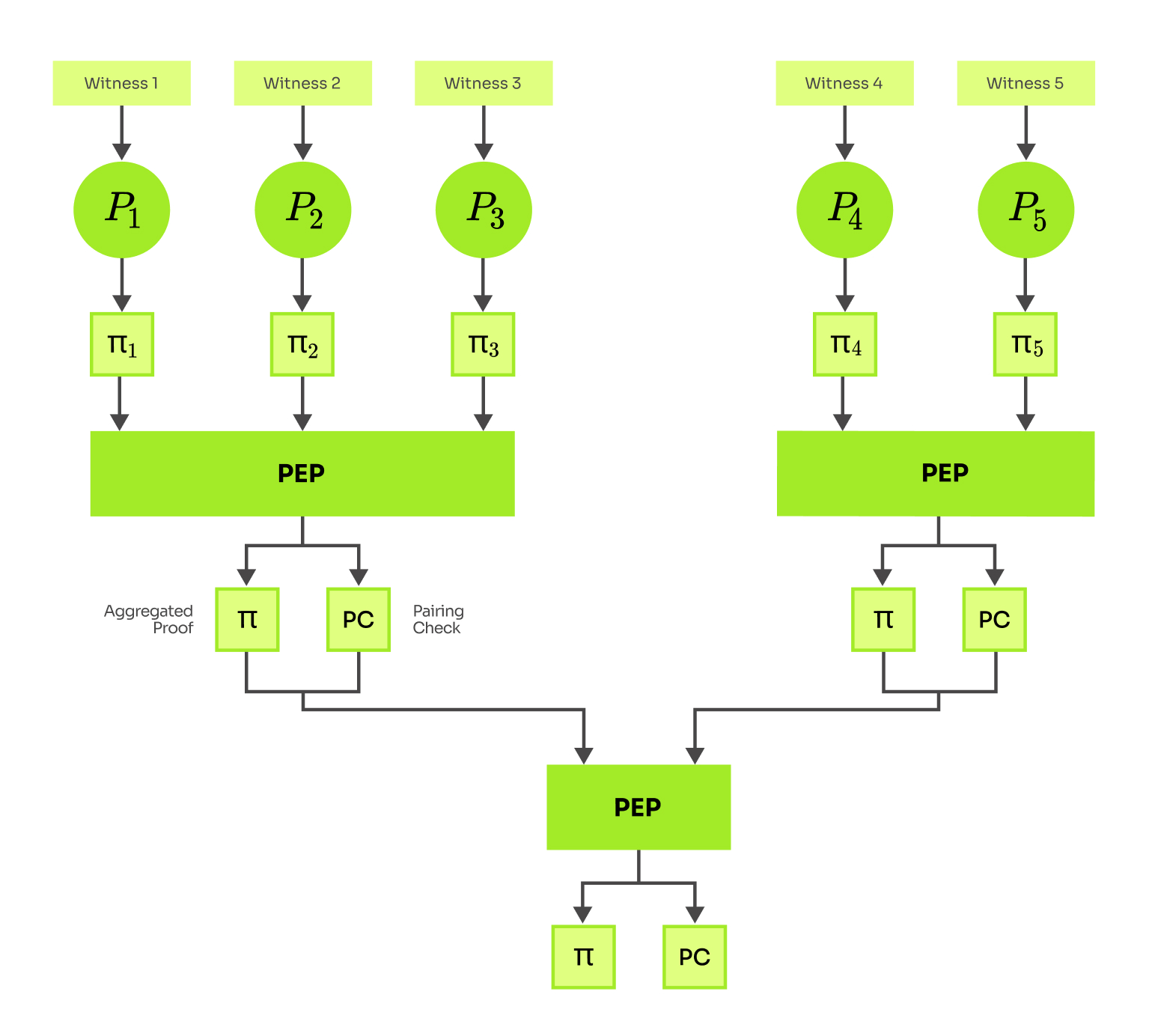
Instead of expressing the pairing check in the circuit we can defer it to a later stage of the proof verification, so the recursive circuit only checks the remaining properties of the proof. Speaking more technically, instead of executing the pairing checks within the circuit, the circuit defers them to an accumulator, which is subsequently exposed as a public input and validated by a verifier. The accumulator is represented by two elliptic curve points and its validation requires computation of a single pairing. This construction was named Pairing-enhanced Plonk (PEP) in Reverie article. I call the proofs produced by PEP pairing-enhanced proofs. Verification of pairing-enhanced proofs has only a small overhead, because a verifier can merge the extra pairing check with the paring check necessary for verification of an underlying vanilla PlonK proof.
PEP aggregation circuit verifies a fixed number of proofs, aggregating them into one pairing-enhanced proof. Although the number of proofs aggregated by the circuit is fixed, the resulting paring-enhanced proofs can be further aggregated, which distinguishes PEP from all aggregation schemes discussed above.
Exclusion of the paring check reduces circuit size dramatically, but there is still a lot of other computations that must be expressed within the circuit: 1. Validation of proof encoding. 2. Recomputation of round challenges derived by a (potentially non-algebraic) hash function. 3. Computation of elliptic curve points for the pairing check. 4. Accumulation of these pairing checks. Let's discuss a particular implementation of the PEP to gain insight into its performance characteristics.
Maze (2022) is an implementation of PEP aggregation by Privacy Scaling Explorations. Aggregation time and memory requirements scale linearly with the number of aggregated proofs. Maze is able to aggregate 50 proofs in 57 minutes and 214 GB RAM peak (on r5a.16xlarge ec2 - v64 CPUS, 512 GB RAM). These substantial hardware demands arise from the size of the aggregation circuit. Nonetheless, Maze remains a viable aggregation scheme resource-wise when compared to a naive recursion approach that incorporates the pairing operation into the recursive circuit.
Aggregation via proof accumulation
Lets discuss fully recursive SNARKs. A pioneer of this world is Halo (2019), designed by Electric Coin Company (Zcash). Halo is not a SNARK, because its proofs are not succinct. For a circuit of size n, Halo produces NARKs (non-succinct SNARK proof) of size O(log n) and verification time O(n). The power of Halo is the full recursivity, allowing a prover to accumulate unlimited amount of NARKs into one and thus to amortize their verification cost. Think about it this way: all NARKs certifying Zcash transactions can be accumulated into one. Verifying one NARK is expensive, but still negligible compared to verification of thousands of individual proofs generated by an arbitrary efficient SNARK.
Recursion is achieved at a cross-over point that is just below 2^17 (~131k) multiplication gates. It also worth mentioning that Halo does not require a trusted setup.
The following work Halo2 (2020) replaces Sonic arithmetization, which was used in Halo, with Plonkish arithmetization, unlocking all PlonK features like custom gates and lookups. Halo2 has detailed documentation and it is used in production to secure shielded transactions in the Zcash blockchain. Proving a 2-in-2-out transaction takes ~2 minutes on a user grade laptop (lenovo, 16 CPUs, 16GB RAM) and the proof has size ~8kb.
Aggregation via folding
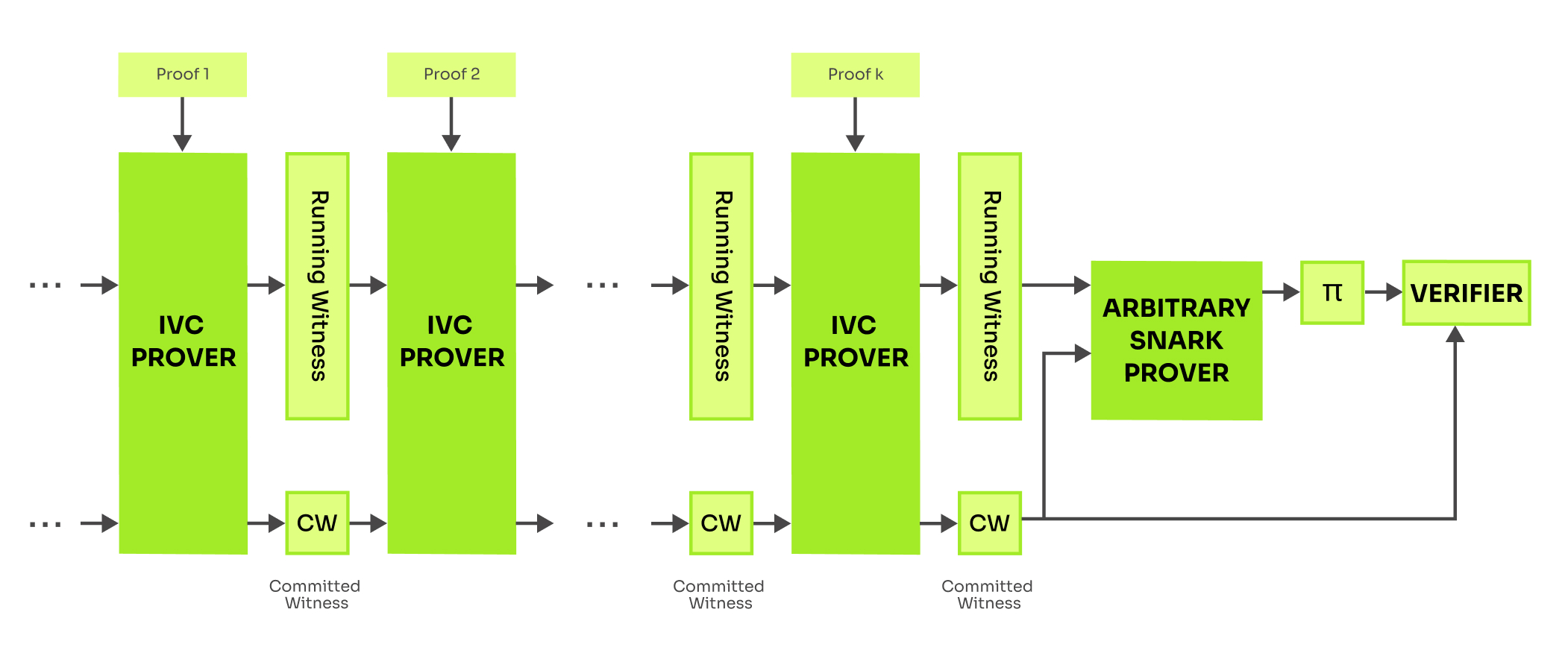
Nova (2020) takes recursion further. Instead of delayed verification (the core of Halo), Nova delays the (optional) succinct proof computation. The core technique of Nova is folding. Folding enables a prover to combine two witnesses w1 and w2 into a new witness w3 of the same size such that proof of w3 proves w1 and w2.
In most applications, Nova is used for Incremental Verifiable Computation (IVC). At each step of the computation, the IVC prover folds a previous running witness with a new witness and proves that the folding was done correctly. At any given point one can verify the latest IVC proof, which, if valid, certifies correctness of the entire execution. Reader can refer to this blog post for a detailed explanation of Nova. In the context of proof aggregation, each individual step of the IVC verifies one proof of a batch.
Definition of IVC requires the size of its proofs to be independent of number of incremental steps. However IVC proofs can be still huge. In case of Nova, the size of IVC proofs is linear in size of the circuit representing an IVC step function. In practical applications, we can stop the IVC at some point, and apply a SNARK on the output, that is on the latest IVC proof, to produce a new proof for the last IVC step which is compact and easily verifiable. The IVC scheme can continue to produce IVC proofs at any given time, independently of the SNARK proof.
The correctness of the folding can be verified by only ~20k constraints (R1CS). As described in CycleFold (2023), this recursive threshold can be further reduced to ~11k constraints. The subsequent works SuperNova (2022) unlocks non-uniform circuit zkVMs and HyperNova (2023) further reduces the prover cost and builds on CSS arithmetization, a generalization of Plonkish, R1CS, and AIR without overheads. Finally, a latticed-based quantum secure adaptation of Nova was described in LaticeFold (February 2024).
SnarkFold (December 2023) offers a detailed description of how to use Nova efficiently to aggregate Groth16 proofs. They introduce a split IVC technique to keep the pairing operation out of the recursive circuit. The aggregated proof has constant size and verification time. SnarkFold is a very promising, but also a fresh article and it is still missing some chapters (PlonK proof aggregation and experimental results).
UniPlonk (2023) offers very detailed analysis of using Nova to aggregate Plonk proofs for different circuits of different sizes and custom gates sets. The overhead of the construction is absolutely negligible and the authors mention support for lookup arguments in the Future Work session.
I believe that SnarkFold and UniPlonk do not exclude each other and thus we will see some synergistic combination of these two in the future.
Finally, Reverie (2023) is a recent end-to-end IVC scheme suitable e.g. for aggregation of validators signatures in the Ethereum network. End-to-end IVC requires communication between individual IVC participants to be minimal. Reverie IVC reaches the communication threshold at ~10kb (for comparison, Nova: ~320kb, STARKs: ~100kb, Plonky2: 42kB). They adopt PEP, CycleFold and smart base-3 decomposition of scalar multiplications in the recursive circuit.
Aggregation via recursive STARKs
STARKs are a particular kind of SNARKs that do not require a trusted setup (T in the acronym stands for “transparent”). I focus on STARKs constructed from Merkle trees and Reed-Solomon proofs of proximity. These constructions yield logarithmic proof size and verification time relative to the circuit size. As they do not rely on elliptic curve arithmetic, they can efficiently validate themselves over a native [2] field when instantiated with an algebraic hash function such as Poseidon. The target field can be relatively small, e.g. 64-bit, which significantly enhances their efficiency on 64-bit architecture machines.
Among numerous STARK candidates and implementations, I spotlight Plonky2 by Polygon Zero as an illustrative example of STARK's capabilities. I selected Plonky2 because I firmly believe that this particular work has notably enhanced the recursion efficiency, consequently broadening the aggregation potential of STARKs. However, it's crucial to note that other contributors have also played pivotal roles in advancing recursive STARKs and there has been public discourse between Polygon Zero and zkSync regarding ownership of certain key concepts along this trajectory.
Plonky2
Plonky2 (2022) is a STARK from Polygon Zero brutally optimized for recursion. It reaches a recursion threshold at incredible ~4k gates. To maintain a fair competition, I point out that these “gates” are quite huge. Plonky2 uses 135 wires (columns) to evaluate Poseidon by a single gate of degree 7 (for comparison, vanilla Plonk uses 3 wires and degree 2 gates).
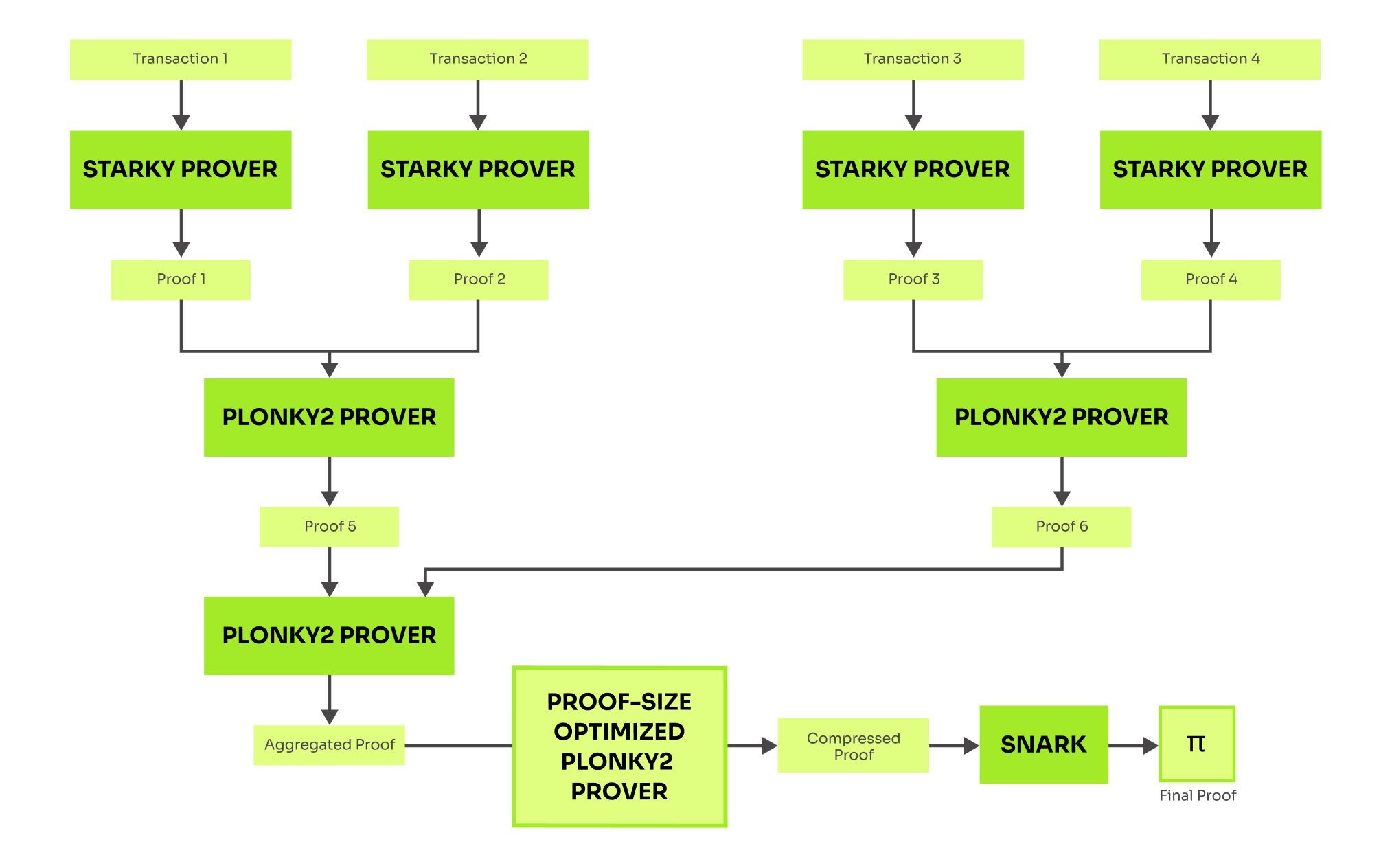
Starky is a highly performant STARK complement of Plonky2. It drops recursion related optimizations to gain maximal efficiency in proving non-recursive statements. To make the situation more complex, there are also different modes of Plonky2 resulting in proving-time vs. proof-size trade-off. In practice, transactions are certified by Starky proofs, which are then aggregated by efficiency-optimized Plonky2, resulting in a large proof. This proof is further compressed by proof-size-optimized Plonky2 and can be further compressed by a SNARK.
The Plonky2 whitepaper remains in draft status, and its implementation has not undergone auditing. According to the draft, the efficiency-optimized Plonky2 generates recursive proofs in 300ms on a 2021 Macbook Air. Proof-size optimized Plonky2 is able to compress any proof to approximately 43 kilobytes in 11.6 seconds, again on a 2021 Macbook Air.
Polygon Zero team is currently working on Plonky3 , which aims to be more modular and universal code base for building STARK based applications. They have already implemented support for M31 field, suggested in Circle STARK (2024) paper by Polygon Zero and Starkware, which holds the potential for additional speed enhancements.
StarkPack
Lastly, I want to mention a very recent blog post starkpack on STARKs packing. StarkPack (Jan 2024) enables the generation of a single proof for the concurrent satisfaction of instances that may originate from different relations, arithmetizations (AIR, Plonkish), and types of FRI-based SNARKs (ethSTARK, Plonky2). The high-level idea is to batch all satisfiability constraints into one by random linear combination. Prover and verifier then perform only one FRI low-degree test across all instances. “Our benchmarks show that for typical traces (2¹⁶ rows, 100 columns), the improvement in verifier time is ~2x, and the reduction of the proof size is ~3x.”
Summary
I have summarized research on proof aggregation over past few years.
- SnarkPack and aPlonK perform algebraic manipulations on a fixed-sized batch of Groth16 (resp. PlonK) proofs, yielding a single log-sized log-verification time proof with respect to the batch size.
- Zexe aggregates proofs over BLS12-377 using a tailored Pinch-Cook curve BW6-761.
- Proof aggregation can be achieved through recursive SNARKs, whose constructions usually necessitate special cryptographic primitives such as specialized elliptic curves and algebraic hash functions.
- Maze keeps pairing check out of a circuit, unlocking recursivity for PlonK at expense of high computational requirements.
- Halo reaches full recursivity by using 2-cycles curves and delayed verification. Halo proofs can be aggregated into one, which makes Halo practical for building fully succinct blockchains. As a bonus, Halo does not require a trusted setup.
- Folding based IVC introduced in Nova seems to be the most effective solution on field of elliptic curves based recursive SNARKs. SnarkFold describes, how to use Nova for efficient proof aggregation. UniPlonK extends it by bringing aggregation of proofs for different circuit with different custom gates. Finally, Reverie optimizes communication overhead between individual IVC participants.
- STARK is a SNARK without requirement of a trusted setup. Well known constructions of STARKs rely on hash functions, code theory and small fields, which make them efficient on standard hardware. STARKs like Plonky2 and Boojum exhibit relatively huge proofs (~43kb). However, this drawback can be mitigated by encapsulating the STARK proof within a SNARK.
As proof aggregation gains prominence in the realm of blockchain scalability, I anticipate emergence of numerous intriguing constructions in the years ahead.
Finally, it's important to remember that while SNARKs are powerful, they can sometimes be unnecessarily heavy-handed tools for certain tasks. For instance, digital signatures can be aggregated using a signature aggregation scheme instead of resorting to a SNARK. For a brief discussion on this topic, readers can refer to the "Do You Need a Zero Knowledge Proof?" article.
For a specific use case like Zcash shielded transactions, I would opt for a proof aggregation scheme or a recursive SNARK based on tailored elliptic curves. However, when constructing a multipurpose solution that involves verifying various SNARKs, non-algebraic hashes, or aggregating signatures of different types - where non-native arithmetic is inevitable - I would certainly leverage a recursive STARK for proof aggregation.
Footnotes
[1]: SNARK is technically an “argument”, not a “proof”. The difference is that arguments may have a small probability of error (incorrect proof that passes verification), though this probability is negligible, while proofs do not allow soundness errors. Despite the fact that the word “argument” captures nature of SNARKs more precisely, the word “proof” became more established in literature.
[2]: A brief explanation of the term “non-native arithmetic”: SNARK claims are expressed as an arithmetic circuits over a given finite field. Claims using native arithmetic of this field can be represented efficiently. For example a circuit over for the claim “I know such that ” has 2 multiplication gates. On the other hand, expressing the claim “I know such that ” by a circuit over will require a bit decomposition of , expressing Montgomery reduction algorithm in the circuit and computing multiplications and additions bit by bit, resulting in a circuit with tens of constraints.
Here is a table summarizing properties of proof aggregation schemes discussed in this post.
| Name | Year | Arithmetization | Target Proof System | Proof Size | Verification | Non-Uniformity | Recursion | Setup | Limitations |
|---|---|---|---|---|---|---|---|---|---|
| 2021 | R1CS | Groth16 | O(log(k)) | O(log(k)) | yes | 2 trusted setups | |||
| 2022 | Plonkish | Plonk | O(log(k)) | O(log(k)) | no | 1 trusted setup | synchronized provers | ||
| 2023 | Plonkish | Plonk | O(1) | O(1) | yes | trusted | |||
| 2019 | Plonkish | Plonk | O(1) | O(1) | yes | ? | trusted | high hardware requirements | |
| 2022 | Plonkish | Plonk | O(1) | O(1) | yes | 21k | trusted | ||
| 2020 | Plonkish | Halo2 | O(log(n)) - 8kb | O(n) | yes | 131k | transparent | ||
| 2020 | R1CS | any | O(n) | O(n) | yes (with SuperNova) | 20k | transparent | non-succinct proofs | |
| 2023 | R1CS (& Plonkish) Groth16, | Plonk | O(1) | O(1) | no | not in the article | trusted | ||
| 2023 | R1CS | any | O(n) | O(n) | probably yes | 11k | transparent | non-succinct proofs | |
| 2021 | Plonkish + AIR | FRI-Stark | O(log(n)^3) - 43kb | O(log(n)^3) | yes | 4k | transparent | huge proofs | |
| 2023 | Plonkish | FRI-Stark | O(1) after compression | O(0) after compression | yes | probably 4k like Plonky2 | transparent + trusted | ||
| 2024 | Plonkish, AIR, RAP… | any FRI-based | O(log(n)) | yes | transparent | aggregator must know witnesses |


