PlonK Deconstructed

Welcome to our blog series about the PlonK protocol. If you've heard a thing or two about SNARKs, zero-knowledge, or PlonK and want to understand how it works, then you are in the right place. We will cover PlonK from the ground up, with focusing on explaining the core ideas and crucial steps. The first couple of posts will cover context and prerequisites.

zk-SNARK

Consider two roles: prover and verifier. The prover tries to convince the verifier that he knows some secret information. To achieve this, we will discuss a special type of proof construction called zk-SNARK: zero-knowledge succinct non-interactive argument of knowledge. We will informally describe each part of the acronym, for a more precise explanation, check out this lecture by Dan Boneh.

Zero-knowledge

In a nutshell, this property allows the prover to prove to the verifier that he know a piece of information without revealing "anything extra" about the information itself. For purposes of this blog, it is sufficient to know that zero-knowledge guarantees that no information is leaked about the secret.

This sounds very abstract and mystic, so let's introduce an example. You have a colorblind friend and two differently colored objects. There is a green ball and a blue ball which look identical to your friend but not to you. You want to prove to your friend that the balls are differently colored, but nothing else. In particular, you do not want to reveal which ball has which color. In this protocol, you are the prover P and your friend is the verifier V.

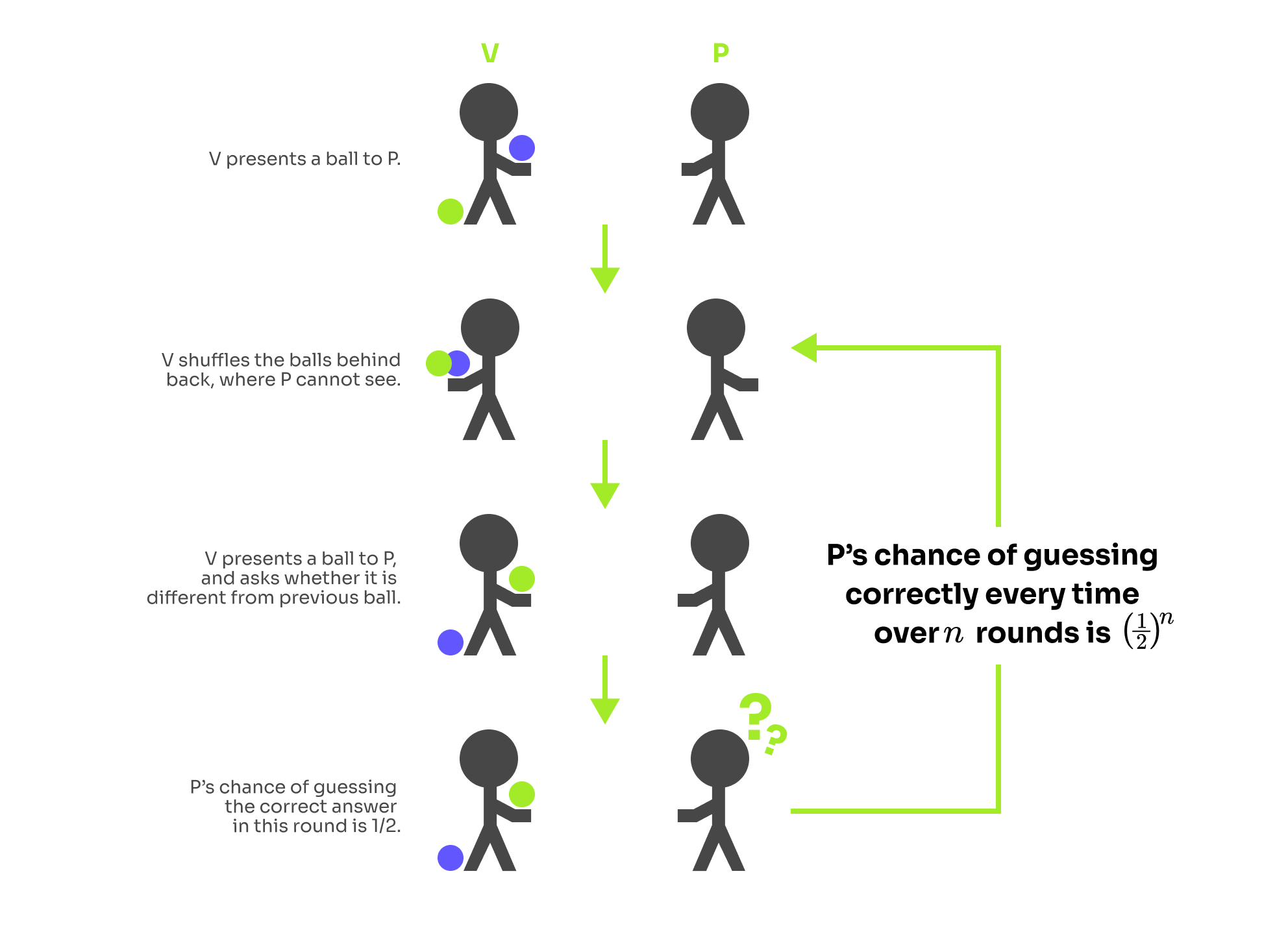
If the balls have different color then you are able to say if your friend switched them or not. On the other hand, if the balls have the same color you need to guess. The probability of successfully guessing is $\frac{1}{2}$, meaning that after 10 rounds your friend can be sure that the balls have different color with probability $1 - \frac{1}{2^{10}} = 0.999023...$ which could be sufficient for most practical purposes.

Zero-knowledge proofs (ZKP) are useful for enhancing privacy and security while maintaining transparency. This might be used in blockchain to prove ownership of certain assets or credentials without revealing sensitive information such as account balances or private keys. Or you might imagine that you want to convince someone that you have a substantial balance on your account without revealing the exact amount, for example when taking the loan. The use cases of zero-knowledge proofs extend far beyond finance and can be applied to various domains where privacy, security, and transparency are essential. The PlonK protocol can be effectively made into zero-knowledge by applying blinding.

Succinct

Succinct is just a fancy word for concise, brief, or compact. This means that the generated proof is small and can be comfortably sent all over the internet. Succinctness also suggests that the proof is easy to verify. In most of the scenarios, there is a heavy prover who does all of the computational work and the verifier just performs lightweight operations to check if the proof is valid. This yields other practical applications. For example, we can delegate expensive computations to un-trusted servers and receive proof showing the integrity of the computations. This proof is short and can be verified more easily.

Non-interactive

Another key part is that these proofs can be non-interactive meaning there is no real-time response expected from the verifier. In the first example, the color-blind verifier was expected to give queries and interact with you. Imagine a (definitely real-world) scenario where you have 50 color-blind friends. You would need to conduct this protocol with each of them. It would be much better if you had just a single proof that you could send to everyone. In non-interactive ZKP the prover generates the proof and gives it to the verifier who decides if it is valid.

Let's look at another simplified example, to get a feeling of how non-interactive ZKP might look. You are at a party with your friends and there is a standard deck of 52 cards, where 26 of them are red and the other 26 are black. You take one random card, assume it is red, and you want to prove to your friends that the card is red without revealing its number. How can you do that? The answer is surprisingly simple. Just show them all of the 26 black cards. This means that there are no more remaining black cards, thus the one that you have picked needs to be red. You have proved the statement without revealing the number of your card. To convince multiple friends you just show each of them all black of the cards. Of course, they must assume, that you are not a cheater and did not take the cards from another deck. In this example, you did not actually calculate the proof but the important thing is that your friends were convinced by a single piece of information that you gave them.

Argument of knowledge

The argument of knowledge should convince the verifier that the prover knows some information. In this series of blogs, we will construct an argument of knowledge that has additional properies mentioned above (zero-knowledge, succinct, non-interactive).

Note that there is a difference between a proof and an argument. Formally, a proof needs to hold no matter what 100%. However, zk-SNARKs produce an argument which is a probabilistic "proofs" that has very small probability of error. In other words, there is a negligible chance that the prover convinces the verifier with a false statement. So, technically we should refer to the proof produced by PlonK as an argument.

zk-SNARK Outline

Say there exists a problem that the prover can solve, and he has a solution. How can he convince the verifier that he indeed knows the solution without revealing it?

We will introduce the approach on the Sudoku game. Suppose there is a partially filled board and there exists a program which checks that no number repeats in any row or column. This program is public and the verifier trusts that this program checks the validity of any Sudoku solution. If the prover can show that the program accepts his solution then the verifier would be convinced that the prover knows a solution. We have just rephrased the problem and now the prover somehow needs to show that running the program indeed succeeds. And that is the topic for the rest of this blog series. Let's generalize this on a diagram:

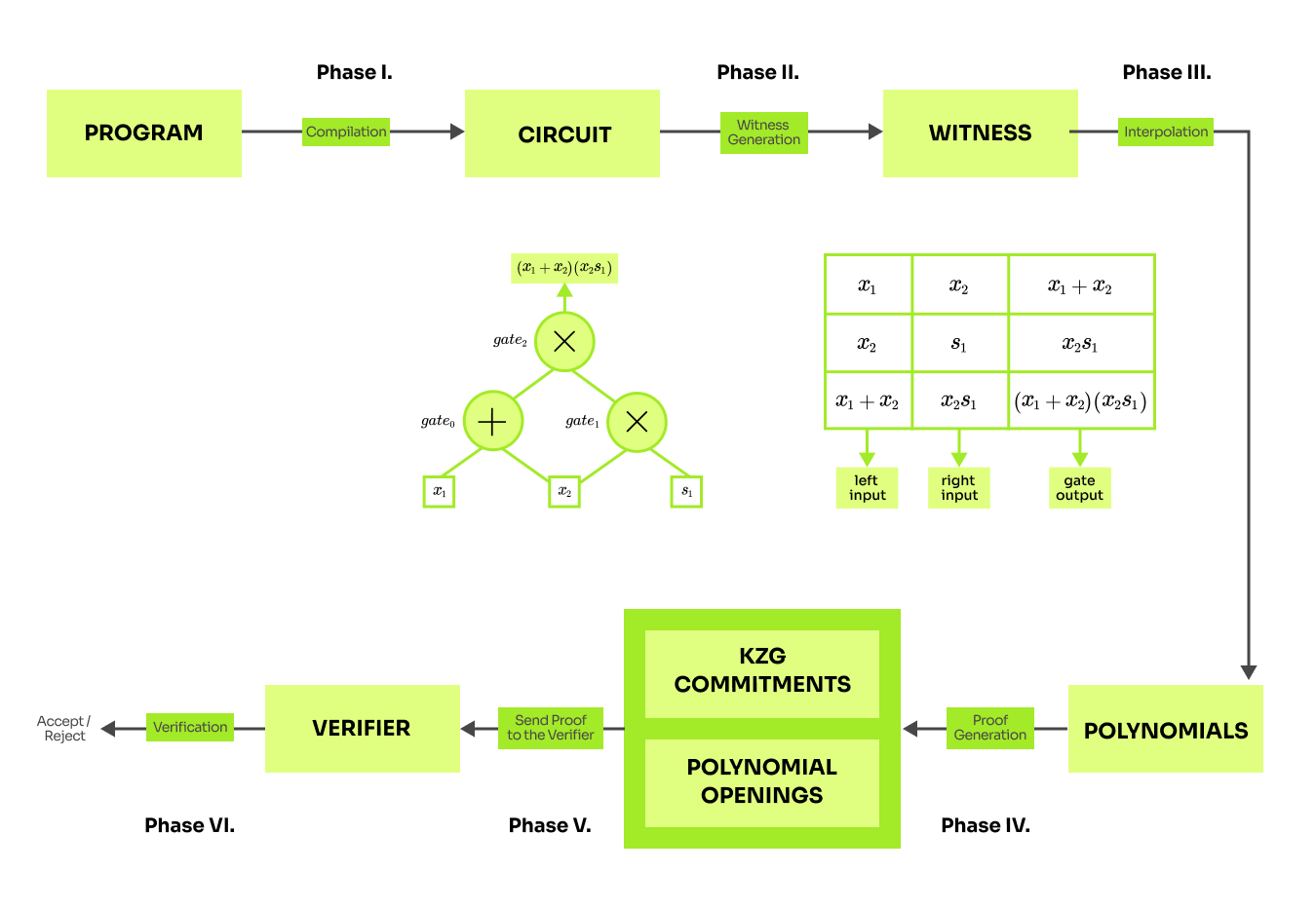
1. Phase I. - Compilation A specified program in the form of code is compiled into a specific series of instructions. This is a standard practice in writing software and it should sound believable. A less common way to think of a program is in the form of a circuit, where gates are instructions and wires represent the flow of values. In the end, each program that is run on a computer needs to be executed on some chip or a processing unit, which in essence is a binary circuit with gates like AND, OR, XOR... But instead of binary operations, we would like to use an arithmetic circuit with operations like addition and multiplication. Luckily, one can always translate a boolean circuit to an arithmetic as explained in Boolean Circuits vs Arithmetic Circuits. As result it is possible to compile a program into an arithmetic circuit.

2. Phase II. - Witness generation The circuit is encoded in the form of a computation table. This table represents the flow of all of the variables in the circuit.

3. Phase III. - Interpolation The values from the table are represented as polynomials. That is namely because polynomials have a lot of useful properties and they will be used to carry out cryptographic proofs.

4. Phase IV. - Proof generation This is the important part, where all of the magic happens. The prover takes the polynomials does some cool tricks and generates proof.

5. Phase V. - Sending the proof (argument) The proof is sent to the verifier for checking.

6. Phase VI. - Verification The verifier analyzes the proof and outputs the result, indicating whether the proof is valid or not.

Again we can illustrate it on the Sudoku game. The prover claims that he knows a valid solution, so he takes the program that checks sudoku validity and rewrites it in terms of polynomials to generate a proof that the program accepts his solution. The proof is sent to the verifier who decides if it is valid. Remember that this proof is weirdly encoded and mangled in polynomials and hard to extract the actual solution.

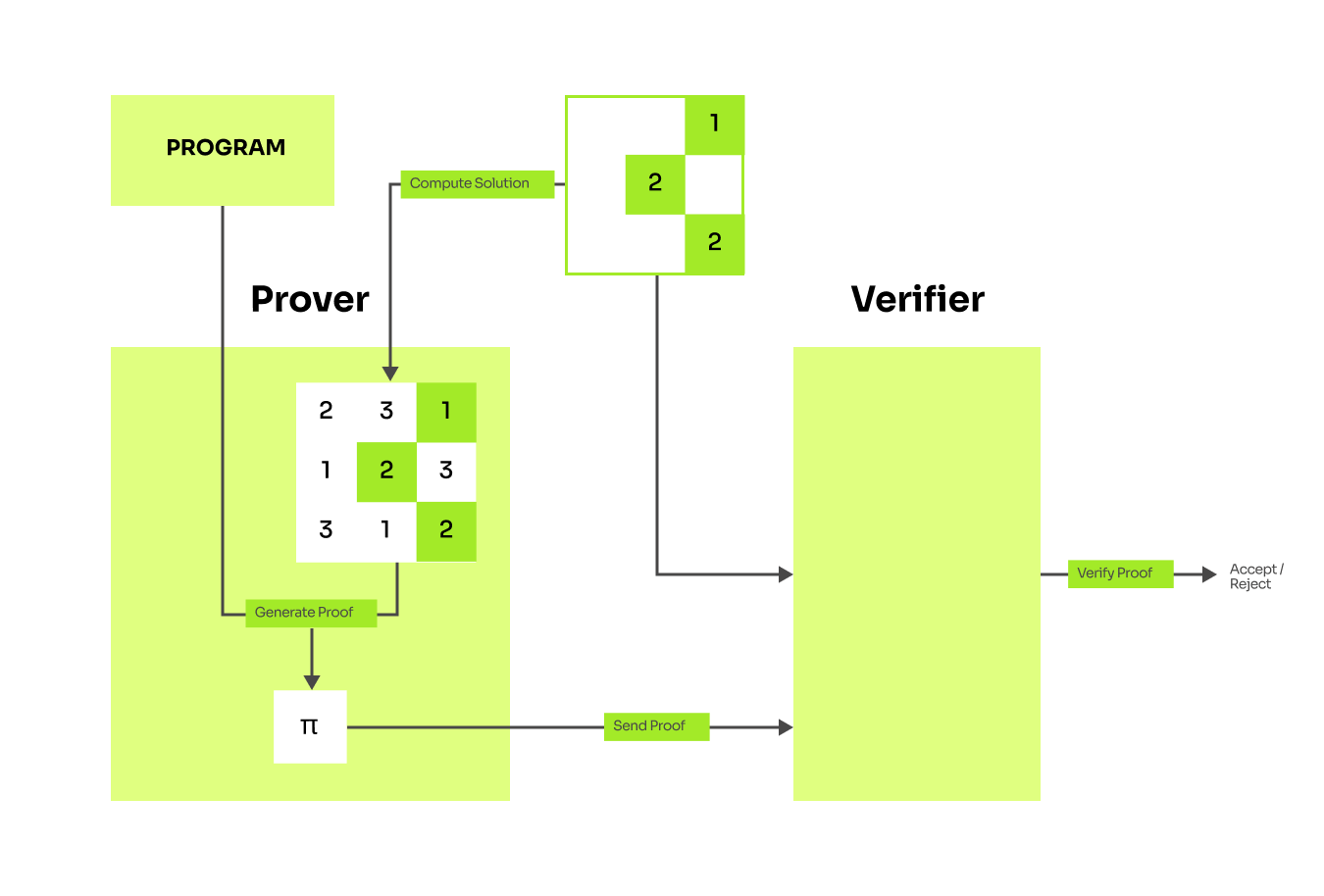
To summarize you should very roughly know what properties zk-SNARKs have. We will be specifically interested in the PlonK protocol. That is because it is a commonly used zk-SNARK and there are many variants building on top of it like Halo2 or HyperPlonk. The PlonK protocol itself was published as eprint in 2019, which is the main source of this blog. Besides we took inspiration from: blog post by David Wong and RisenCrypto blogs.

In the next post, we will talk about Phase II., where you will learn how to construct equations from a circuit. Then we will cover commitment schemes, followed by proof generation, which is split into 5 rounds.

List of the PlonK blog posts:

• 1: Overview
• 2: Arithmetization
• 3: Math Preliminaries
• 4: KZG
• 5: Setup
• 6: Round 1
• 7: Round 2
• 8: Round 3
• 9: Round 4
• 10: Round 5
• 11: Verification

If you have any suggestions or improvements to this blog, send an e-mail to contact@maya-zk.com