Round 2

In this post, we will talk about the copy constraints that ensure the "circuit is wired correctly". We will describe how to handle the copy constraints and build the permutation polynomial from the ground up.

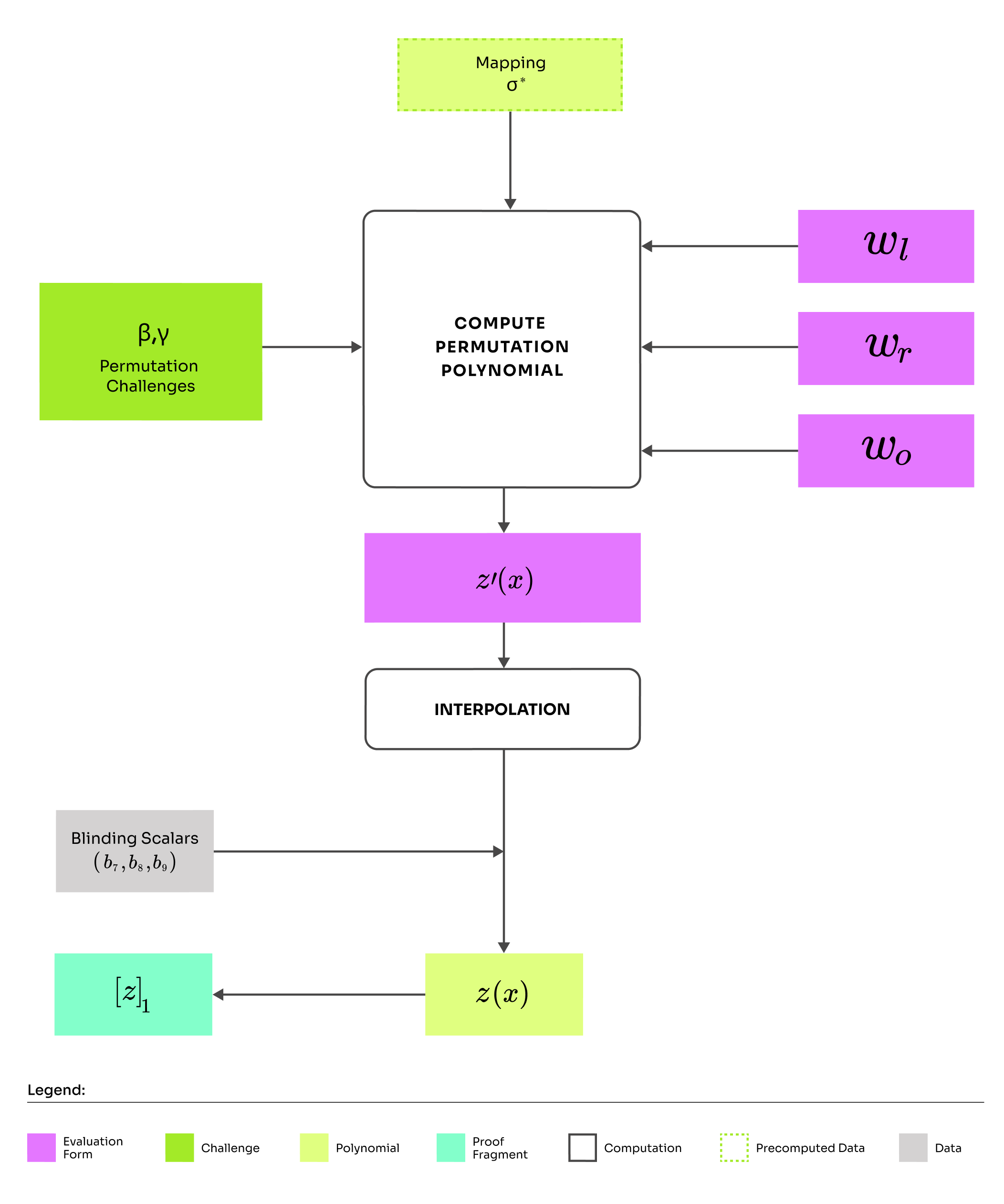
Round overview:

1. Receive permutation challenges $\beta = \mathcal{H}(transcript, 0), \gamma = \mathcal{H}(transcript, 1)$

2. Compute permutation polynomial $z(x)$

3. Compute and output commitment $[z]_1 \in \mathbb{G}_1$

Permutations

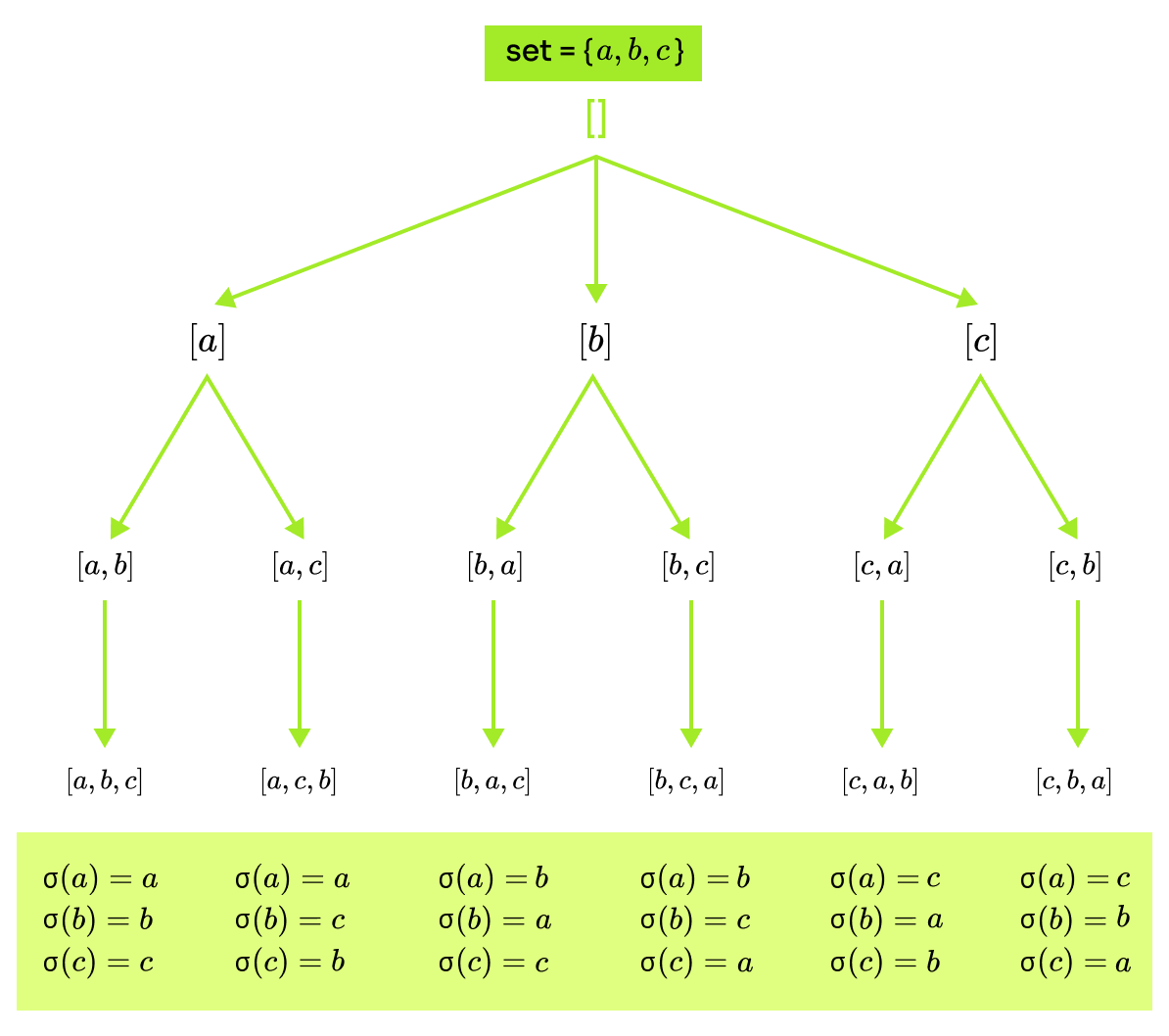
To start from the very basics, a permutation is an ordering of a set. Take a set of elements $S = (a, b, c )$ then $[c, b, a]$ is a permutation, and so is $[b, a, c]$ but not $[b, b, c]$. A permutation is mapping $\sigma: S \rightarrow S$ that express some shuffling. Below are expressed all permutations for $S$.

Why is this useful? If you look back at the computation table from arithmetization, it is clear that some cells must be equal. Each gate represents some computation, and the edges of the graph or "wires" define the flow of the variables. By connecting $gate_i$ to $gate_j$, we express that the output of $gate_i$ is passed as input to $gate_j$. It should hold output of $gate_i$ $=$ input to $gate_j$. How can the prover convince the verifier that these constrints are satisfied?

Put the variables into boxes such that in each box, all variables have the same value. We can say that we create equivalence classes, depending on how the gates are wired. In each box, the variables are somehow ordered. We will want to construct a permutation function $\sigma$ that changes the order of the elements in each box. The function $\sigma$ is usually implemented as a rotation of the elements in the equivalence classes.

Consider witness vector $w$ which has size $3n$ and is composed of $w_l, w_r, w_o$ such that $w = {w_{l_1}, \ldots ,w_{l_n}, w_{r_1}, \ldots ,w_{r_n}, w_{o_1}, \ldots ,w_{o_n}}$. This is how the permutation $\sigma$ would look for the example diagram from arithmetization.

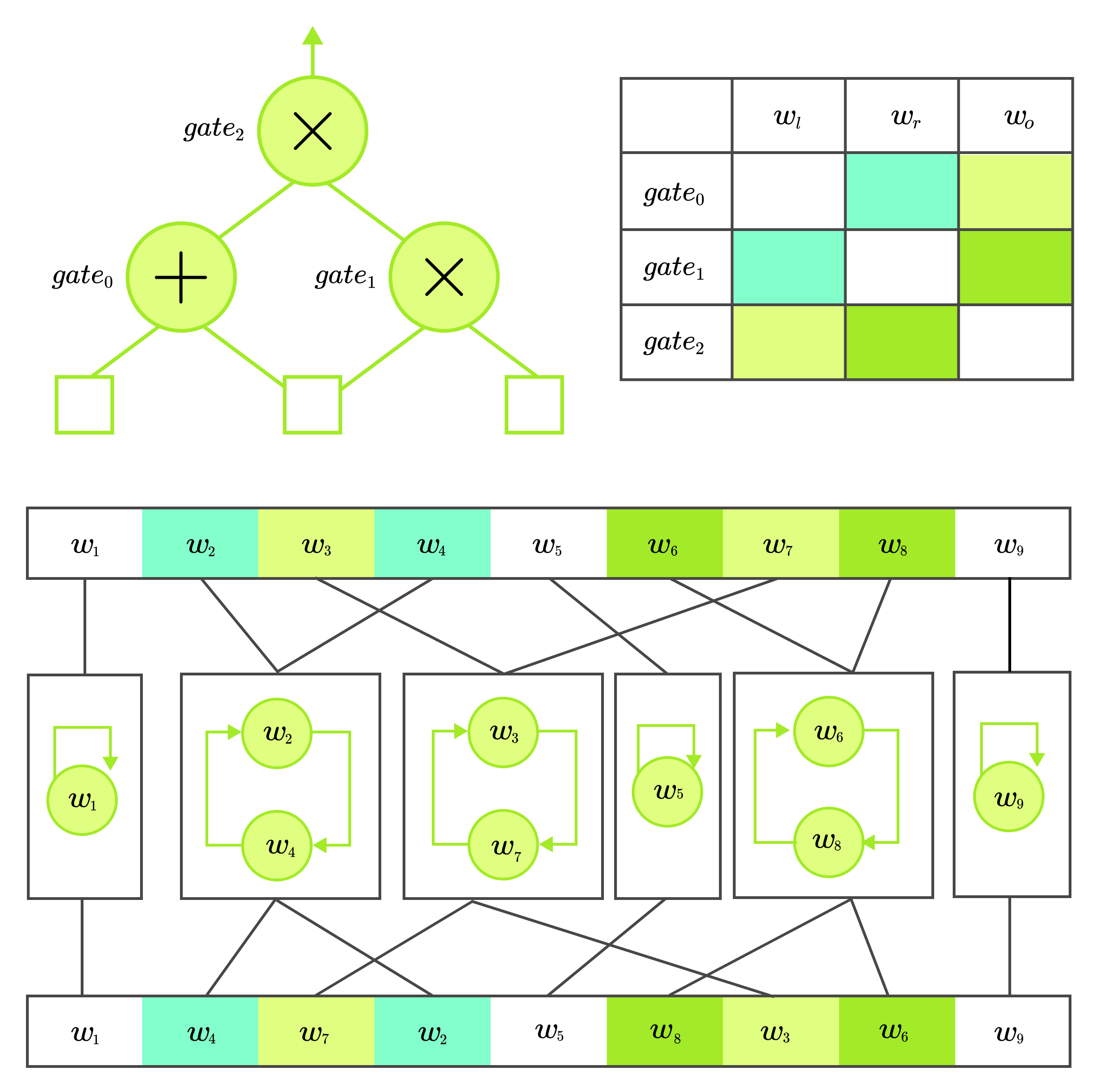
No matter on the input of the circuit the values in the equivalence class must always contain the same value. This specific circuit thus has copy constraints $$w_2 = w_4, w_3 = w_7, w_6 = w_8$$

We can prove that the copy constraints hold by showing that $w_i = \sigma(w_i)$ holds for every index $i$. Say there is constraint $w_i = w_j = w_k = w_l$ and we get: $$\vdots$$ $$w_i = \sigma(w_i) \rightarrow w_i = w_j$$ $$w_j = \sigma(w_j) \rightarrow w_j = w_k$$ $$w_k = \sigma(w_k) \rightarrow w_k = w_l$$ $$w_l = \sigma(w_l) \rightarrow w_l = w_i$$ $$\vdots$$

Naturally, the expressions above are satisfied if and only if $w_i = w_j = w_k = w_l$. That is the core idea that will be used in the permutation check. Now, we would like to effectively use this observation in the protocol.

In the following section, we will build the permutation polynomial from the ground up. We will first show how to check that two vectors are permutations of each other. Then, we will try to detect a specific permutation on a vector. And finally, we will see how to check permutations across multiple vectors.

Permutation check

An enemy gives you two vectors $p = [p_1, p_2 \ldots p_n], q = [q_1, q_2 \ldots q_n]$, and you need to quickly decide if they are permutations of each other. You could naively compare the elements one by one, but that is too slow. Instead you can try to aggregate the vectors into a single value and perform, something like a product check: $$p_1 \times p_2 \times \ldots \times p_n \stackrel{?}{=} \sigma(q_1) \times \sigma(q_2) \times \ldots \times \sigma(q_n)$$

This approach satisfies correctness, because multiplication is commutative. However it does not satisfy soundness, meaning the check can pass even if the vectors are not equal. For example, vectors $[1,6]$ and $[2,3]$ would pass the check, but they are not permutations of each other. What if the sample an element $\gamma$ and perform a variation of the product check:

$$(p_1 + \gamma) \cdot (p_2 + \gamma) \ldots (p_n + \gamma) \stackrel{?}{=} (\sigma(q_1) + \gamma) \cdot (\sigma(q_2) + \gamma) \ldots (\sigma(q_n) + \gamma)$$ $$\prod_{i = 1}^n p_i + \gamma \stackrel{?}{=} \prod_{i = 1}^n \sigma(q_i) + \gamma$$

This check is also correct because of the commutativity of multiplication, but what about the soundness? The whole trick is to think of this expression in terms of polynomials where each side of the equation is a polynomial evaluated at a randomly selected point $\gamma$. From the previous post we know that that if this check succeeds, then the polynomials are equal with very high probability.

Intra-vector check

This is really nice, but the problem is that no specific permutation is enforced. How can we enforce a permutation that is defined as rotation on the equivalence classes? We have two vectors and a permutation $\sigma: H \rightarrow H$. The trick is to encode the elements as $(\text{index}, \text{value})$ where for the index, we will use the elements of evaluation domain $H$. Below is an example where the permutation swaps the last two elements.

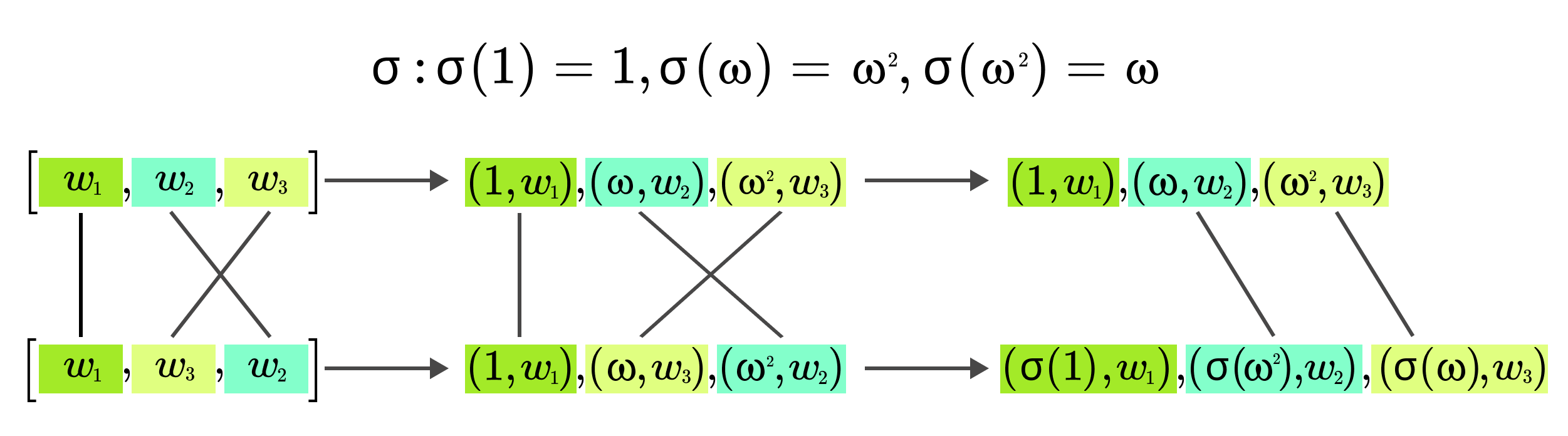
Okay, but the permutation check above relies on the fact that we were comparing polynomials, so we somehow need to write the tuples as polynomials. We will construct a random linear combination, therefore $(\omega^{i-1}, w_i)$ becomes $w_i + \beta \omega_{i-1}$ where $\beta$ is randomly sampled.

Why can we use this encoding of tuples? (optional section)

In order to use this check safely in the protocol, we need to be sure that $$(a, b) = (a', b') \iff a + \beta b = a' + \beta b'$$

The answer is polynomials. Notice that $a + \beta b$ is a linear polynomial with coefficients $a, b$ evaluated at $\beta$, and so is $a' + \beta b'$ just with different coefficients. We know that comparing polynomials at a randomly selected point gives us a good guarantee that the polynomials are equal. So we conclude that if the random linear combinations are equal, then with very high probability also, the tuples are equal.

Now we can put everything together. We will use the permutation check and enforce specific permutation by encoding tuples as random linear combinations. This finalizes the check for a specific permutation on a single vector.

$$(w_1 + \beta 1 + \gamma) \ldots (w_n + \beta \omega^{n-1}+ \gamma) \stackrel{?}{=} (w_1 + \beta \sigma(1) + \gamma) \ldots (w_n + \beta \sigma(\omega^{n-1}) + \gamma)$$ $$\prod_{i = 1}^n w_i + \beta \omega^{i-1}+ \gamma \stackrel{?}{=} \prod_{i = 1}^n w_i + \beta \sigma(\omega^{i-1}) + \gamma$$ $$1 \stackrel{?}{=} \frac{\prod*{i = 1}^n w_i + \beta \omega^{i-1}+ \gamma}{\prod*{i = 1}^n w_i + \beta \sigma(\omega^{i-1}) + \gamma}$$

To sum it up, we have shown that the copy constraints of the arithmetic circuit could be represented as a permutation. First we tried to perform effective check of arbitrary permutation and then check for a specific permutation. Once again, the answer lay in converting everything to polynomials. The last obstacle in constructing the permutation polynomial is that we need to be able to check permutation across multiple vectors.

Inter-vector check

In this case, we will want to check the permutation across vectors $w_l, w_r, w_o$, which are columns of the computation table described in arithmetization. Each of $w_l, w_r, w_o$ has size $n$ and we will concatenate them into $w = {w_{l_1}, \ldots,w_{l_n}, w_{r_1}, \ldots,w_{r_n}, w_{o_1}, \ldots,w_{o_n}}$ which has size $3n$. The domain $H$ is no longer sufficient for indexing $w$ because it has size $n$. We will solve this by using larger $H' = H \cup (k_1H) \cup (k_2H)$, where $k_1, k_2 \in \mathbb{F}_p$ are chosen such that all elements in $H, k_1H, k_2H$ are distinct.

Here we will use the $\sigma^*: [1, 2, \ldots, 3n] \rightarrow H'$ from setup. It also performs rotation on the equivalence classes, we just need to extend the domain and image to accommodate $3n$ values. Using the same ideas as before, we construct the check for the inter-vector case.

$$1 \stackrel{?}{=} \prod_{i=1}^{n} \frac{p(i)}{q(i)}$$

$$p(i) = (w*{i} + \beta \omega^i + \gamma)(w*{n+i} + k,[object Object],{2n+i} + k*2\beta\omega^i+ \gamma)$$ q(i) = (w*{i} + \beta \sigma^_ (i) + \gamma)(w_{n+i} + \beta \sigma^_ (n+i) + \gamma)(w_{2n+i} + \beta \sigma^* (2n+i) + \gamma)

This expression might be undefined when $q(i)$ is 0. However, this only happens with negligible probability. When it happens, the protocol is instructed to abort and repeat with other randomly sampled $\beta, \gamma$.

The Permutation Polynomial

How can we convince the verifier that this check succeeds? We cannot give him the values to compute the check, because he would discover $w$, which violates zero-knowledge. Moreover the verifier should run in time smaller than $\log{n^k}$, so this computation would be too heavy. Unsurprisingly, we will solve this problem by constructing the permutation polynomial, which is defined as:

$$z(\omega^0) = 1$$ $$i \in [1 \ldots n-1]: z(\omega^i) = \prod*{j=1}^{i} \frac{p(j)}{q(j)}$$

The essential idea of the permutation check remains the same. We are taking the product of ratios, where the numerator represents the former set and the denominator represents the permuted set. If each of these ratios is 1 that means the copy constraints are satisfied. How do we construct this polynomial? We will proceed as usual and interpolate the values over the domain $H$. $$\left(z(\omega), z(\omega^2), z(\omega^3) \ldots z(\omega^{n-1})\right)$$ $$\left(\frac{p(1)}{q(1)}, \frac{p(1)p(2)}{q(1)q(2)}, \frac{p(1)p(2)p(3)}{q(1)q(2)q(3)}, \ldots, \prod_{i=1}^{n-1} \frac{p(i)}{q(i)} \right)$$

$$z'(x) = \sum_{i=1}^{n-1} L_{i}(x) \prod_{j=1}^i \frac{p(j)}{q(j)}$$

To enforce that the permutation polynomial evaluates to 1 on $\omega^0$ we add the Lagrange basis $L_0(x)$. To finish it up, we add blinding. This time, we will need a blinding polynomial of degree 2 because the permutation polynomial will be used in two proofs of polynomial openings ($W*\mathfrak{z}, W*{\mathfrak{z} \omega}$) in round 5.

$$z(x) = (b_7x^2 +b_8x +b_9)Z_H(x) + L_0(x) + z'(x)$$

Great, and that is all there is to the permutation polynomial. The prover can happily finish round 2 by committing to the permutation polynomial. In the next post about round 3, we will show how to construct the quotient polynomial and prove that the permutation polynomial was computed correctly.

List of the PlonK blog posts:

• 1: Overview
• 2: Arithmetization
• 3: Math Preliminaries
• 4: KZG
• 5: Setup
• 6: Round 1
• 7: Round 2
• 8: Round 3
• 9: Round 4
• 10: Round 5
• 11: Verification

If you have any suggestions or improvements to this blog, send an e-mail to contact@maya-zk.com