Round 3

We have introduced the permutation polynomial which should guarantee that copy constraints are satisfied. By construction of the quotient polynomial the prover will show that the permutaiotn polynomial is valid and the gate constraints hold. But first, we will introduce a check to verify that some polynomial is zero over a specified domain.

Round overview:

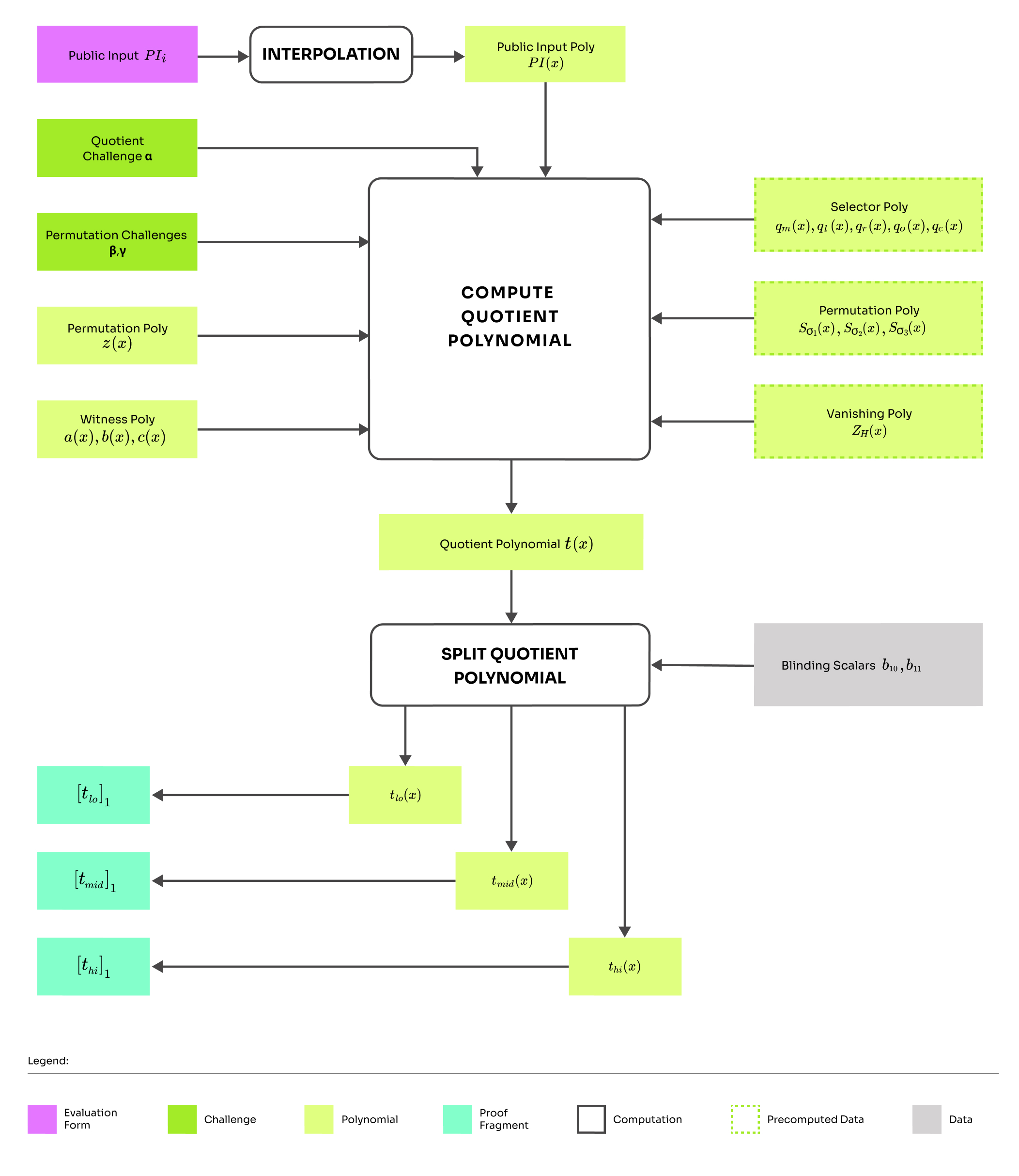
1. Compute quotient challenge $\alpha = \mathcal{H}(transcript)$

2. Compute quotient polynomial $t(x)$

3. Split $t(x)$ into polynomials of smaller degree

4. Compute and blind polynomial parts $t_{lo}(x), t_{mid}(x), t_{high}(x)$

5. Commit and output $[t_{lo}]_1$, $[t_{mid}]_1$, $[t_{hi}]_1$

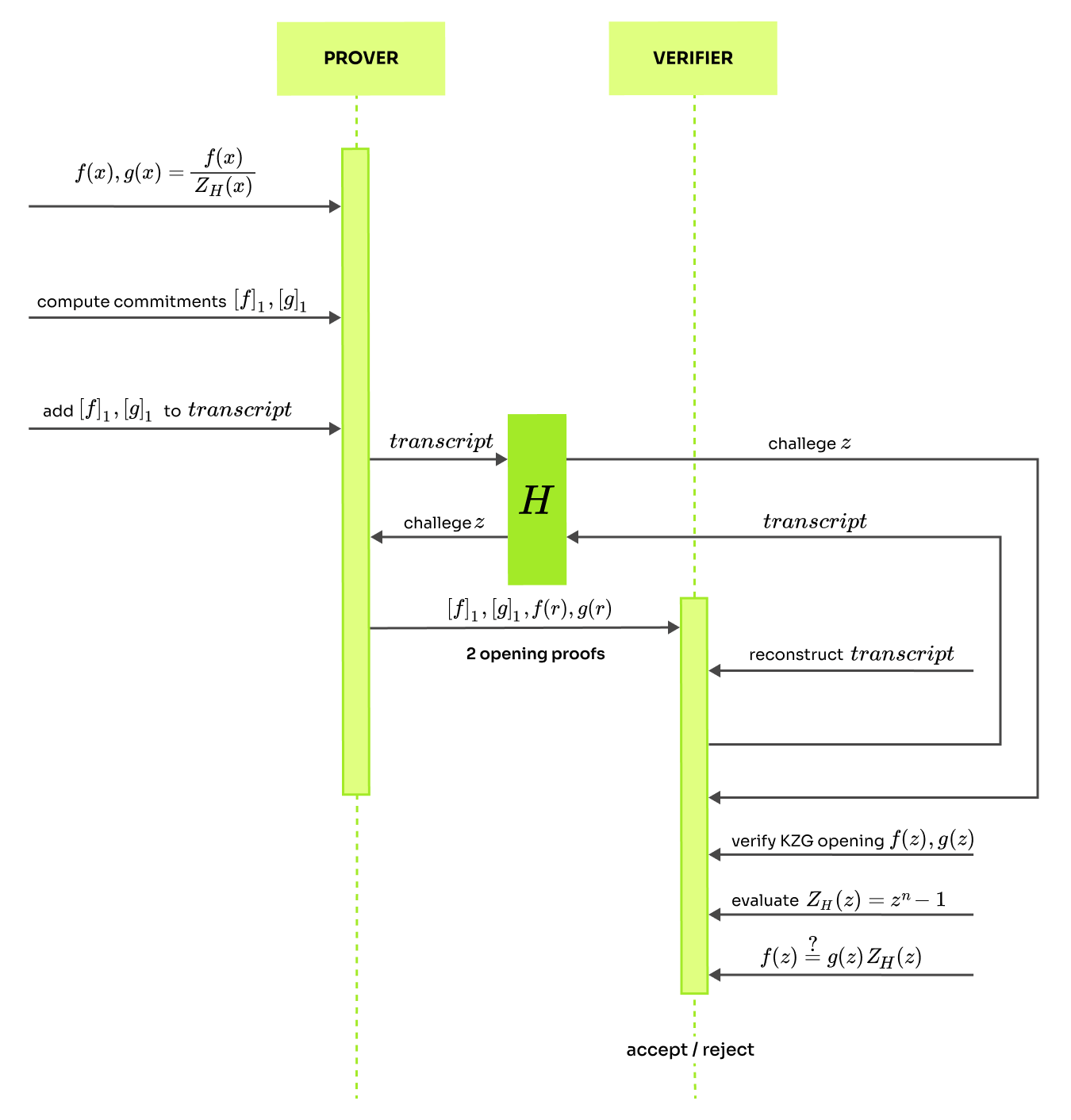
Zero test

In this round, we will need to prove that some polynomials evaluate to 0 over the whole domain $H$. Luckily, we have all the tools that we need. If some polynomial $f(x)$ is zero on $H$, then every element of $H$ has to be a root, which means it can be factored as $f(x) = g(x)Z_H(x)$ where $Z_H(x)$ is the vanishing polynomial. This implies that a polynomial $f(x)$ is zero on $H$ if and only if it is divisible by $Z_H(x)$. The observation enables to change the zero check into a divisibility check. To verify that $f(x) = g(x)Z_H(x)$, the verifier checks evaluation at a random point $z$ as $f(z) \stackrel{?}{=} g(z)Z_H(z)$. The security of this check was discussed in the preliminaries. To make sure that $f(z) \text{ and } g(z)$ are evaluations of $f(x) \text{ and } g(x)$ we will use the KZG polynomial commitment scheme.

This check is sound (does not pass if $f(x)$ is not zero on $H$), because if the polynomial $f(x)$ is not zero on the whole domain $H$, then it cannot be divided by $Z_H(x)$. As result, the prover cannot provide $g(x)$ that would satisfy $f(x) \stackrel{?}{=} g(x)Z_H(x)$. To put this into context, this test can be made into a standalone, non-interactive protocol that uses the KZG polynomial commitment scheme. Below is a detailed diagram of how it works. We use a random oracle $\mathcal{H}$ to generate the challenge $z$ based on a transcript.

Checking permutation polynomial

In the previous round, we computed and committed to the permutation polynomial $z(x)$. However, we did not prove that it was computed correctly. Specifically we have promised that $z(\omega^0) = 1$, otherwise it is cumulative product $z(\omega^i) = \prod_{1 \leq j < i} p(j) / q(j)$. This is equivalent to checking:

1. $(z(x)-1)L_0(x) = 0$
2. $z(x)\tilde{p}(x) = \tilde{q}(x)z(x\omega)$

where $\tilde{p}(x), \tilde{q}(x)$ are: $$\tilde{p}(x) = (a(x) + x\beta + \gamma)(b(x) + k_1 x\beta + \gamma)(c(x) + k_2 x\beta + \gamma)$$ $$\tilde{q}(x) = (a(x) + S_{\sigma_1}(x)\beta + \gamma)(b(x) + S_{\sigma_2}(x) \beta + \gamma)(c(x) + S_{\sigma_3}(x)\beta + \gamma)$$

Why are the above checks sufficient? (optional section)

1. work?

• if $x = \omega^0$ then $L_0(\omega^0)$ evaluates to 1 and we are left with $(z(\omega^0) - 1) = 0$ which is 0 only if $z(\omega^0) = 1$ effectively checking what we wanted
• if $x \neq \omega^0$ the Lagrange basis $L_0(x)$ evaluates to 0 and we get $0 = 0$

2. check?

The second statement checks if the permutation polynomial was computed as a cumulative product $z(\omega^i) = \prod_{1 \leq j < i} p(j) / q(j)$. The claim is that if $\forall i \in [n]: z(\omega^i)\tilde{p}(\omega^i) = \tilde{q}(\omega^i)z(\omega^{i+1})$ then the polynomial was computed as specified by the protocol. We can prove this claim inductively by showing that it holds for $i+1$ supposing it holds for $i$: $$z(\omega^{i+1})\tilde{f}(\omega^{i+1}) = \tilde{g}(\omega^{i+1})z(\omega^{i+2})$$ $$\prod_{1 \leq j < i+1} \frac{f(\omega^j)}{g(\omega^j)} \tilde{f}(\omega^{i+1}) = \tilde{g}(\omega^{i+1})z(\omega^{i+2})$$ $$\frac{\tilde{f}(\omega^{i+1})}{\tilde{g}(\omega^{i+1})} \prod_{1 \leq j < i+1} \frac{f(\omega^j)}{g(\omega^j)} = z(\omega^{i+2})$$ $$z(\omega^{i+2}) = \prod_{1 \leq j < i+2} \frac{f(\omega^j)}{g(\omega^j)}$$

The functions $\tilde{p}(x), \tilde{q}(x)$ are similar to the $p(x), q(x)$ from the previous round. But why do we perform the check with $\tilde{p}(x), \tilde{q}(x)$ instead of $p(x), q(x)$? The functions $p(x), q(x)$ are computed in evaluation form from the values of $w$ and $\sigma^*$ while $\tilde{p}(x), \tilde{q}(x)$ are computed from interpolations of $w$ and $\sigma^*$. This means that $\tilde{p}(x), p(x)$ and $\tilde{q}(x), q(x)$ agree on the evaluation domain $H$. $$\forall i \in [0, 1 \ldots n-1]: p(i) = \tilde{p}(\omega^i) \text{ and } q(i) = \tilde{q}(\omega^i)$$

The permutation polynomial was calculated in the evaluation form and consequently interpolated. To check that the prover used correct values for the witness $w$, the verifier can check the permutation polynomial against $a(x), b(x), c(x)$, which interpolate $w$. The important thing is that the commitments $[a]_1, [b]_1, [c]_1$ were calculated before the permutation polynomial, so the prover is bounded to the witness before he starts constructing the permutation polynomial.

Computing quotient polynomial

The quotient polynomial $t(x)$ might look complicated at first sight, but it is only an aggregation of the arithmetic gate check and the permutation copy constraint check. We will split it into $t_1(x), t_2(x), t_3(x)$ such that $t(x) = t_1(x) + t_2(x) + t_3(x)$.

$$t_1(x) = (a(x)q_{l}(x) + b(x)q_{r}(x) + c(x)q_{o}(x) + a(x)b(x)q_{m}(x) + PI(x) + q_{c_i})\frac{1}{Z_H(x)}$$ $$t_2(x) = (\tilde{p}(x)z(x)) - (\tilde{q}(x)z(\omega x))\frac{\alpha}{Z_H(X)}$$ $$t_3(x) = (z(x)-1)L_1(x)\frac{\alpha^2}{Z_H(x)}$$

1. The first term $t_1(x)$ might feel familiar. This is the gate constraint introduced in the arithmetization. This term ensures that each gate is evaluated correctly. To be more specific, if it evaluates to zero at $\omega^i$ that means the gate $i$ is computed correctly.

2. The term $t_2(x)$ corresponds to the 2. check from the previous section. The check was introduced as: $\tilde{p}(x)z(x) = \tilde{q}(x)z(x\omega)$. But after rearranging we get $$\tilde{p}(x)z(x) - \tilde{q}(x)z(x\omega) = 0$$

3. Finally, the last term is the 1. check from the previous section checking $z(\omega^0) = 1$.

One common thing for each term is the division by the vanishing polynomial $Z_H(x)$ and multiplication by some $(1, \alpha, \alpha^2)$. The division $Z_H(x)$ by application of the zero test described above. The multiplication by $(1, \alpha, \alpha^2)$ ensures that the quotient polynomial evaluates to zero only if all of the separate terms evaluate to zero.

Why do we multiply by $(1, \alpha, \alpha^2)$? (optional section)

We might get an unsound protocol if we compute the quotient polynomial without multiplication by a random $\alpha$. For example when $t_1(x) = 0, t_2(x) = -t_3(x)$ then the quotient polynomial $t(x)$ evaluates to 0 even though $t_2(x) \text{ and } t_3(x)$ are not valid. The prover might want to use this to cheat the protocol. We can prevent it by multiplying the terms with a random linear combination $(1, \alpha, \alpha^2)$ which is a standard technique for batching checks in cryptography.

The important thing is that the commitments to polynomials $a(x), b(x), c(x), z(x)$ are part of the transcript, which affect the choice of the challenge. Since, it is not possible to discover the challenge before the commitments it is hard to cheat the protocol as in the example above.

If $t_1(x) = t_2(x) = t_3(x) = 0$ then naturally $t_1(x) +\alpha t_2(x) + \alpha^2 t_3(x) = 0$. However, if some of the terms $t_1(x), t_2(x), t_3(x)$ is non-zero, there is only a negligible probability that after multiplication by a random linear combination $t(x)$ will be 0.

Splitting quotient polynomial

Amazing, now we know how to construct the quotient polynomial. However, the resulting polynomial degree is too big. We want our polynomials to have the maximum degree of $n$. Why? We assumed so in the setup while creating SRS. However, it is possible to split $t(x)$ into smaller polynomials $t_{lo}'(x), t_{mid}'(x)$ of degree $< n$ degree and $t_{hi}'(x)$ of degree at most $n+5$ such that: $$t(x) = t_{lo}'(x) + x^nt_{mid}'(x) + x^{2n}t_{hi}'(x)$$

Why is the degree of the quotient polynomial $3n+5$? (optional section)

The degree of $t(x)$ is determined by $t_2(x)$ where we multiply wire polynomials $a(x), b(x), c(x)$ and permutation polynomial $z(x)$. Each of the wire polynomials has degree bound $n+1$, and the permutation polynomial has $n+2$, which makes it $4n+5$, but $t_2(x)$ is also divided by $Z_H(x)$ of degree $n$. Therefore, the degree bound of the quotient polynomial $t(x)$ is $3n+5$.

The quotient polynomial $t(x)$ has a degree at most $3n+5$, which means it can be written as $t(x) = c_0 + c_1x \ldots c_{3n+5}x^{3n+5}$. Then we can split as:

$$t_{lo}'(x) = c_0 + c_1 x + c_2 x^2 \ldots c_{n-1}x^{n-1}$$

$$t_{mid}'(x) = \frac{c_{n}x^{n} + c_{n+1}x^{n+1} \ldots c_{2n-1}x^{2n-1}}{x^n}$$

$$t_{hi}'(x) = \frac{c_{2n}x^{2n} + c_{2n+1}x^{2n+1} \ldots c_{3n+5}x^{3n+5}}{x^{2n}}$$

This looks better, but we forgot something. Before committing, we want to blind the polynomial so that the protocol remains zero-knowledge. Here the prover chooses two random blinding scalars $b_{10}, b_{11} \in \mathbb{F}_p$ and blinds the polynomial as: $t_{lo}(x) = t_{lo}'(x) + b_{10}x^n, t_{mid}(x) = t_{mid}'(x) - b_{10} + b_{11}x^n, t_{hi}(x) = t_{hi}'(x) - b_{11}$. Finally, we calculate the commitments $[ t_{lo} ]_1$, $[ t_{mid} ]_1$, $[ t_{hi} ]_1$ and move to the next round, where we will calculate polynomial openings and show a neat trick to minimize the number of openings.

List of the PlonK blog posts:

• 1: Overview
• 2: Arithmetization
• 3: Math Preliminaries
• 4: KZG
• 5: Setup
• 6: Round 1
• 7: Round 2
• 8: Round 3
• 9: Round 4
• 10: Round 5
• 11: Verification

If you have any suggestions or improvements to this blog, send an e-mail to contact@maya-zk.com