Verification algorithm

We have covered the whole prover algorithm in the previous posts. Now, we would like to show how to check the validity of the provided argument $\pi$. Besides the common preprocessed input, there is also verifier preprocessed input consisting of commitments to public polynomials: $[q_m]_1, [q_l]_1, [q_r]_1, [q_o]_1, [q_c]_1,$ $[S_{\sigma_1}]_1,$ $[S_{\sigma_2}]_1,$ $[S_{\sigma_3}]_1$ . The polynomials are public, therefore the verifier can compute the commitments.

The first part of the verifier algorithm performs sanity checks on the commitments and openings, reconstructs the transcript to calculate the challenges, and evaluates some public polynomials.

1. Validate commitments $([a]_1, [b]_1, [c]_1, [z]_1,$ $[t_{lo}]_1,$ $[t_{mid}]_1,$ $[t_{hi}]_1,$ $[W_{\mathfrak{z}}]_1,$ $[W_{\mathfrak{z} \omega}]_1)$ $\in \mathbb{G}_1$

   checks that the provided commitments are in the correct group. The group is constructed from an elliptic curve, so for each commitment, the elliptic curve equation must hold $y^2 = x^3 + ax + b$

2. Validate evaluations $(\bar{a}, \bar{b}, \bar{c},$ $\bar{S}_{\sigma_0},$ $\bar{S}_{\sigma_1},$ $\bar{z}_\omega)$ $\in \mathbb{F}_p$ is even easier than the previous check. The verifier must ensure that each evaluation is in $[0, 1, 2, \ldots, p - 1]$.

3. Validate public inputs $PI_i \in \mathbb{F}_p$ check that the public inputs are elements of the field the same way as in the case above.

4. Compute challenges $\beta, \gamma, \alpha, \mathfrak{z}, v, u \in \mathbb{F}_p$. In an interactive case, this is easy since the verifier is the one who generated the challenges. In non-interactive case, challenges are generated by a random oracle based on the transcript of the protocol as described previously. The verifier can get the challenges by reconstructing the transcript and querying the random oracle. Since the random oracle is deterministic, the verifier should get the same challenges as the prover.

5. Evaluate vanishing polynomial $Z_H(\mathfrak{z}) = \mathfrak{z}^n - 1$. vanishing polynomial is public.

6. Evaluate Lagrange basis $L_1(\mathfrak{z}) = \prod_{k \in H, k \neq \omega} \frac{\mathfrak{z}-k}{\omega-k}$ the Lagrange basis is also public.

7. Evaluate public input polynomial evaluation $PI(\mathfrak{z})$ constructs the public input polynomial and evaluates it at $\mathfrak{z}$.

The following steps are more interesting and involve batched KZG verification. We will show a high-level idea of how it works. The more formal explanation can be found in section 3.4 of the KZG paper.

Batched polynomial commitment scheme

Say that the committer knows polynomials $f_1, f_2$ and wants to prove evaluations at randomly selected challenge $f_1(\mathfrak{z}) = v_1, f_2(\mathfrak{z}) = v_2$. Rather than checking each claim independently, it is possible to batch them. We will perform a batched check using uniformly randomly selected $u$ as $$u f_1(\mathfrak{z}) + f_2(\mathfrak{z}) \stackrel{?}{=} u v_1 + v_2$$

Naturally, this approach is correct because if $f_1(\mathfrak{z}) = v_1, f_2(\mathfrak{z}) = v_2$, then for any $u$, the equality needs to hold. Moreover, the approach is also sufficiently sound. Notice that we can think about both $u f_1(\mathfrak{z}) + f_2(\mathfrak{z})$ and $u v_1 + v_2$ as linear functions with variable $u$. If two linear functions are not identical, they have at most one crossing point, so the soundness error of the batching is at most $1 / \mathbb{F}_p$, which is sufficiently low. So, with a very high probability, it holds that: $$f_1(\mathfrak{z}) = v_1, f_2(\mathfrak{z}) = v_2 \iff u f_1(\mathfrak{z}) + f_2(\mathfrak{z}) =u v_1 + v_2$$

This means it is sufficient to verify the opening of the batched polynomial. Now, we will use a similar trick as in the linearization by defining $f_{batch}(x) = u f_1(x) + f_2(x)$. The commitment $[f_{batch}]_1$ can be computed as $u[f_1]_1 + [f_2]_1$. So the prover just needs to send commitments $[f_1]_1, [f_2]_1$, opening $\bar{f}_{batch}$ and proof of the opening. Why is this better? The prover must only calculate one opening proof to the batched polynomial $f_{batch}$. If we performed this separately, there would need to be two opening proofs for $f_1, f_2$.

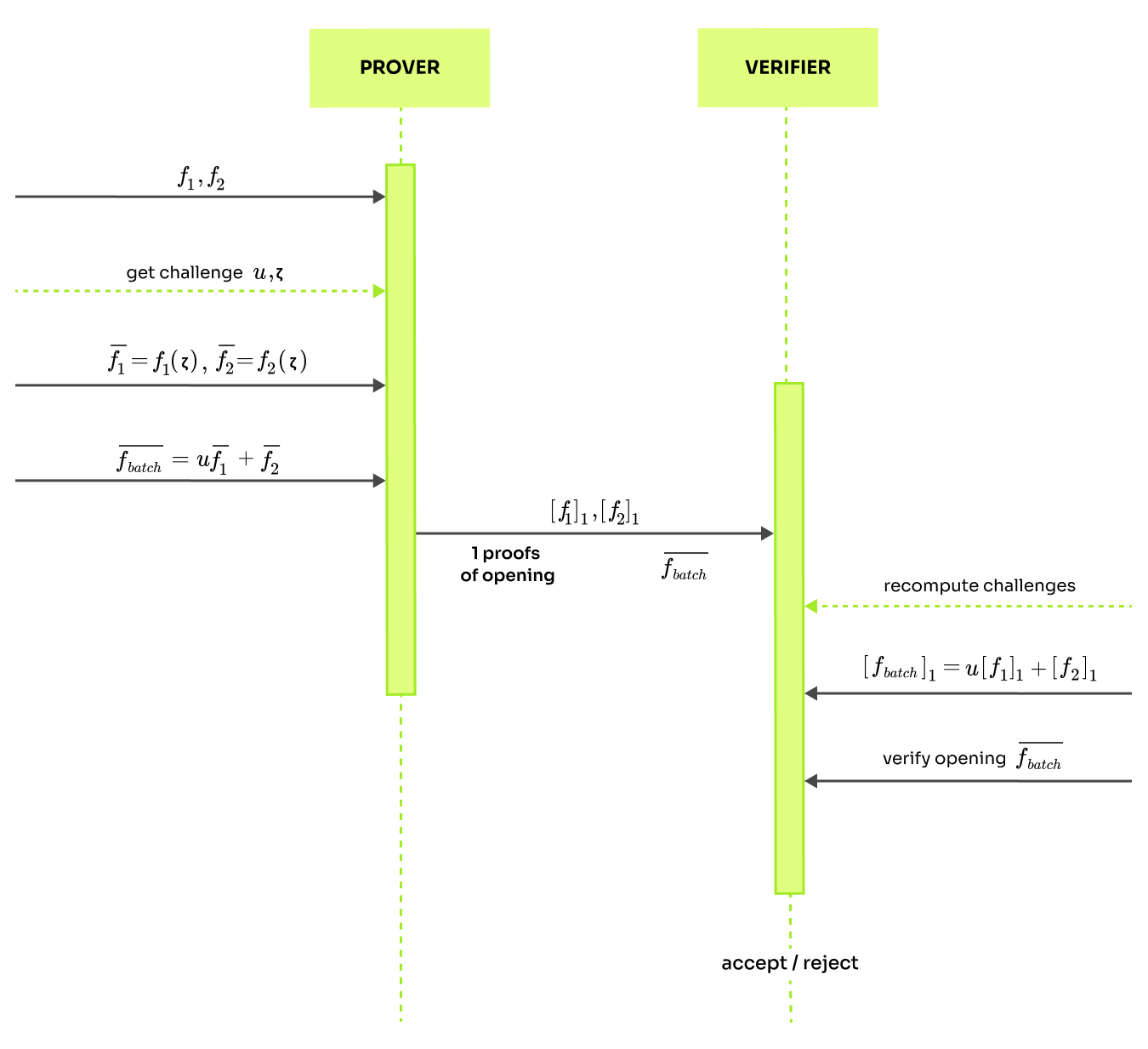
Detailed explanation of the batched KZG can be found at blog by RisenCrypto, and a more general approach is described in the post PCS Mutli-proofs.

Batched Plonk verification

In the round 5 proofs of opening are consensed into $W_{\mathfrak{z}}(x)$ and $W_{\mathfrak{z}\omega}(x)$. They can be written in a simplified way as $W_{\mathfrak{z}}(x) = F(x) / (x - \mathfrak{z})$, $W_{\mathfrak{z}\omega}(x) = E(x) / (x - \mathfrak{z}\omega)$ and after some rearranging we get: $$xW_{\mathfrak{z}}(x) = \mathfrak{z} W_{\mathfrak{z}}(x) + F(x)$$ $$xW_{\mathfrak{z}\omega}(x) = \mathfrak{z}\omega W_{\mathfrak{z}\omega}(x) + E(x)$$

Now, we add a batch challenge $u$ to batch-equation as described in the previous section and sum the two equations together. $$x(W_{\mathfrak{z}}(x) + uW_{\mathfrak{z}\omega}(x)) = \mathfrak{z} W_{\mathfrak{z}}(x) + u\mathfrak{z}\omega W_{\mathfrak{z}\omega}(x) + F(x) + uE(x)$$

In steps 8-11 of the verification algorithm, the verifier calculates the commitments to $[E]_1, [F]_1$. The final step checks the above identity using batched KZG-style verification with commitments and pairings:

$e([W_\mathfrak{z}]_1 + u \cdot$ $[W_{\mathfrak{z}\omega}]_1)$ $, [\tau]_2$ $) = e(\mathfrak{z} \cdot [W_\mathfrak{z}]_1 +$ $+ u\mathfrak{z}\omega \cdot [W_{\mathfrak{z}\omega}]_1 + [F]_1 - [E]_1, [1]_2)$

This validates all the statements about the circuit described in the arithmetization. And that is all. Besides understanding the protocol, you hopefully also learned something about modern cryptography.

List of the PlonK blog posts:

• 1: Overview
• 2: Arithmetization
• 3: Math Preliminaries
• 4: KZG
• 5: Setup
• 6: Round 1
• 7: Round 2
• 8: Round 3
• 9: Round 4
• 10: Round 5
• 11: Verification

If you have any suggestions or improvements to this blog, send an e-mail to contact@maya-zk.com