Round 5

Previously, we have seen how to perform linearization tricks. We will use this knowledge in the finale of the prover algorithm. All constraints are combined in this round to generate the argument/proof $\pi$.

1. Compute opening challenge $v \in \mathbb{F}_p = \mathcal{H}(transcript)$

2. Compute linearisation polynomial $r(x)$

3. Compute opening proof polynomial $W_{\mathfrak{z}}(x)$

4. Compute opening proof polynomial $W_{\mathfrak{z}\omega}(x)$

5. Calculate commitments $[W_{\mathfrak{z}}]_1$, $[W_{\mathfrak{z}\omega}]_1$

6. Return proof $\pi$

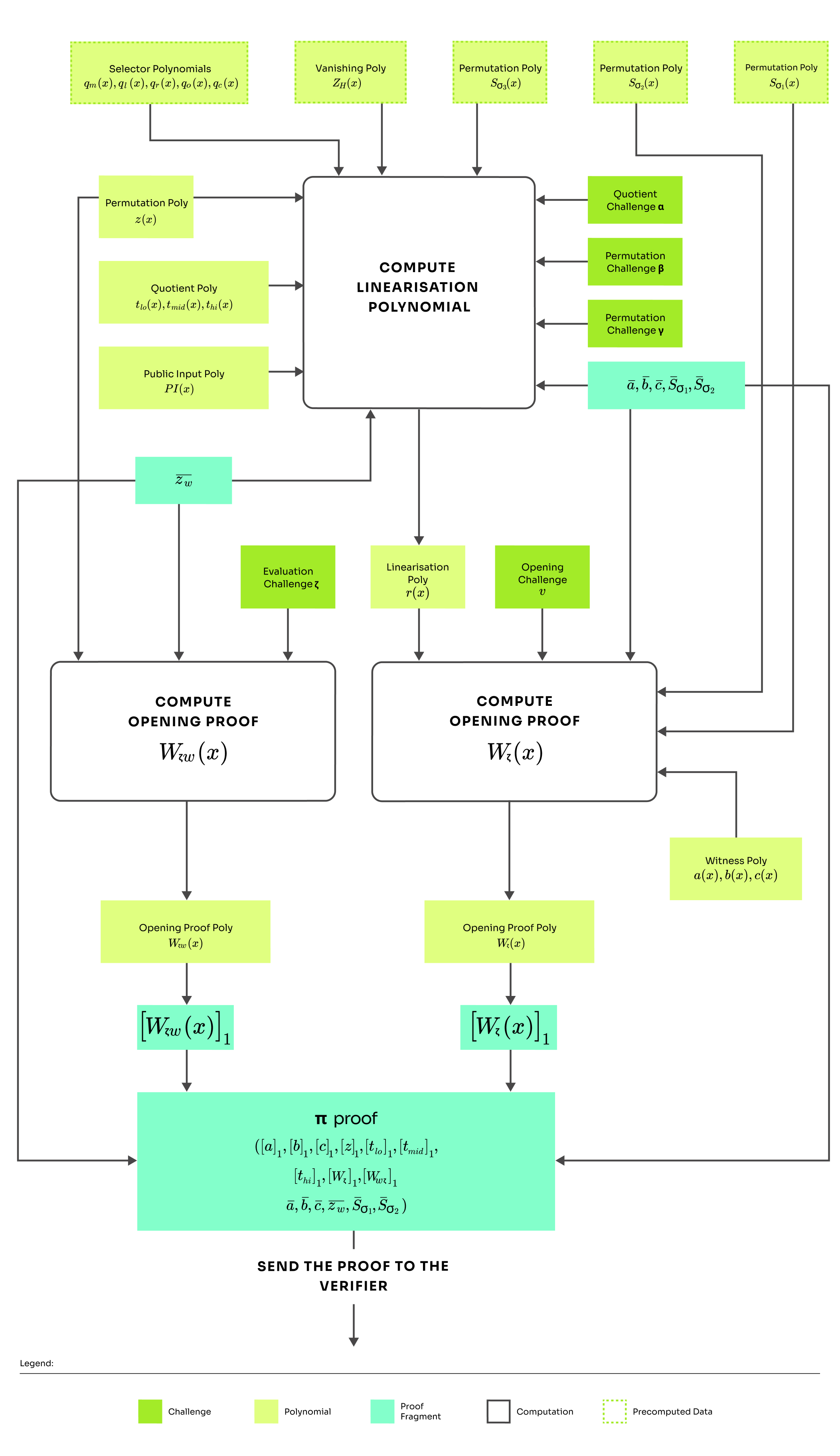
Linearisation polynomial

Recall from the third round that the quotient polynomial $t(x)$ was split into 3 parts to reduce the degree, such that it holds: $$t_{lo} + x^{n}t_{mid}(x) + x^{2n}t_{hi} = \frac{t_1(x) + \alpha t_2(x) + \alpha^2t_3(x)}{Z_H(x)}$$ $$0 = t_1(x) + \alpha t_2(x) + \alpha^2 t_3(x) - Z_H(x)(t_{lo} + x^{n}t_{mid}(x) + x^{2n}t_{hi})$$

This is the base of how we will construct the linearisation polynomial $r(x)$. Some of the terms in $t_1(x), t_2(x), t_3(x)$ are substituted with the openings $\bar{a}, \bar{b}, \bar{c}, \bar{z_\omega}$ $\bar{S}_{\sigma_1},$ $\bar{S}_{\sigma_2}$ which the prover calculated in the round 4. The linearisation polynomial can be expressed as:

$$r(x) = r,[object Object],{lo}(x) + \mathfrak{z}^n t*{mid}(x) + \mathfrak{z}^{2n} t*{hi}(x))$$

• $r_1(x)$ represents linearised arithmetic gate check corresponding to $t_1(x)$ in the quotient polynomial $t(x)$.

  $r_1(x) = \bar{a}\bar{b}q_m(x) + \bar{a}q_l(x) + \bar{b}q_r(x) + \bar{c}q_o(x) + PI(\mathfrak{z}) + q_c(x)$

• $r_2(x)$ is linearised $t_2(x)$ from the quotient polynomial $t(x)$. It represents the second check of the permutation polynomial.

  $r*2(x) = (\bar{a} + \beta \mathfrak{z} + \gamma)(\bar{b} + \beta k_1 \mathfrak{z} + \gamma)(\bar{c} + \beta k_2 \mathfrak{z} + \gamma)z(x)$ -(\bar{a} + \beta \bar{s},[object Object],1} + \gamma) (\bar{b} + \beta \bar{s},[object Object],2} + \gamma) $(\bar{c} + \beta S*{\sigma,[object Object],{\omega}$

• $r_3(x)$ corresponds to $t_3(x)$, which represents the first check of the permutation polynomial

  $r_3(x) = (z(x) -1)L_0(\mathfrak{z})$

If the prover computed everything according to the protocol description $r(x)$ is zero over the whole domain $H$. Notice which polynomials are evaluated (denoted with the horizontal line). As described in the previous round, the linearization polynomial can contain polynomial additions and multiplication by a constant, but not multiplication of two polynomials. And that is exactly what we are trying to achieve. The openings are picked so that there is not a single polynomial multiplication. This allows us to use the linearization trick, and as a result, the prover does not need to send the commitment $[r]_1$ because the verifier can calculate it independently.

The big picture is that the prover is trying to prove: $0 = t_1(x) + \alpha t_2(x) + \alpha^2 t_3(x) - Z_H(x)(t_{lo} + x^{n}t_{mid}(x) + x^{2n}t_{hi})$. If he did it naively, he would need to send an opening to every polynomial. However, thanks to the linearization trick, we can minimize the number of openings, thus also reduce the proof size.

Opening proof polynomial

The prover must provide two opening proofs - one for opening at $\mathfrak{z}$ and the second for opening at $\mathfrak{z}\omega$.

First opening proof polynomial

The polynomial $W_{\mathfrak{z}}$ proofs openings of polynomials $r(x), a(x), b(x), c(x), S_{\sigma_1}, S_{\sigma_2}$ in $\mathfrak{z}$. Analogous to the KZG we will transform the equality check into divisibility check by constructing an opening proof polynomials: $$\frac{r(x)}{x-\mathfrak{z}} \stackrel{proves}{\rightarrow} r(\mathfrak{z}) = 0$$ $$\frac{a(x) - \bar{a}}{x-\mathfrak{z}} \stackrel{proves}{\rightarrow} a(\mathfrak{z}) = \bar{a}$$ $$\frac{b(x) - \bar{b}}{x-\mathfrak{z}} \stackrel{proves}{\rightarrow} b(\mathfrak{z}) = \bar{b}$$ $$\ldots$$

Finally, these are combined using random linear combination $(1, v, v^2, v^3, v^4, v^5)$ where $v$ is the opening challenge. The batching is based on the same principle as described in the round 3. This yields the first opening proof polynomial:

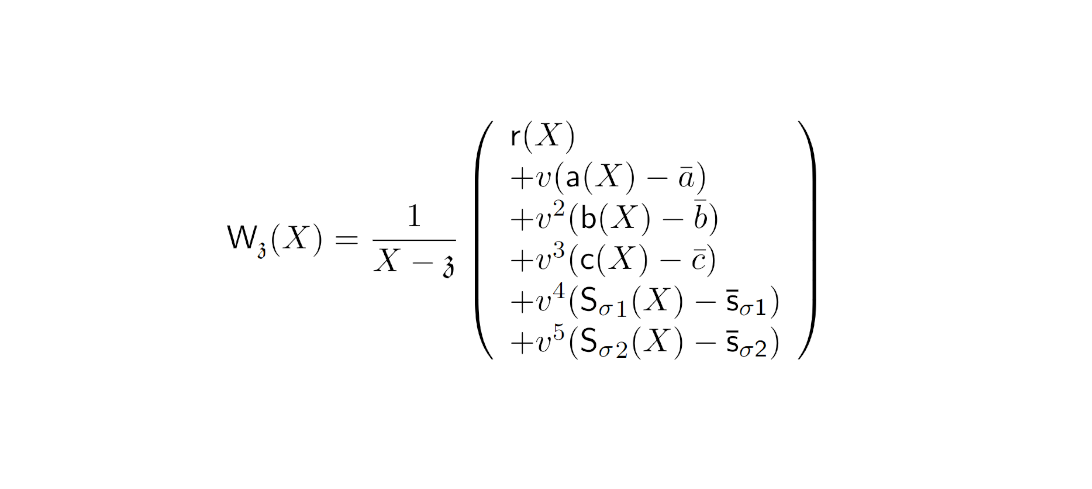
Second opening proof polynomial

Lastly, the prover constructs an opening proof polynomial for $z(x)$ on $\mathfrak{z}\omega$:

$$W_{\mathfrak{z}\omega}(x) = \frac{z(x)-\bar{z}_{\omega}}{x - \mathfrak{z}\omega}$$

The only difference $W_{\mathfrak{z}}(x)$ it that this polynomial proves opening in $\mathfrak{z}\omega$ instead of $\mathfrak{z}$

Return Proof

At the end of this round, the prover can finally send the whole proof: $\pi = ([a]_1, [b]_1, [c]_1, [z]_1$ $[t_{lo}]_1,$ $[t_{mid}]_1,$ $[t_{hi}]_1,$ $[W_{\mathfrak{z}}]_1,$ $[W_{\omega\mathfrak{z}}]_1,$ $\bar{a}, \bar{b}, \bar{b},$ $\bar{S}_{\sigma_1}$ $\bar{S}_{\sigma_2})$

We have looked at the prover side of the algorithm. In the last post, we will continue with the verifier's algorithm.

List of the PlonK blog posts:

• 1: Overview
• 2: Arithmetization
• 3: Math Preliminaries
• 4: KZG
• 5: Setup
• 6: Round 1
• 7: Round 2
• 8: Round 3
• 9: Round 4
• 10: Round 5
• 11: Verification

If you have any suggestions or improvements to this blog, send an e-mail to contact@maya-zk.com