Maya ZK Blog

Polynomial commitment scheme is a crucial component of the protocol, which is why understanding it will explain many steps in the protocol. In this part, we will briefly explain commitment schemes and then look at the KZG procedures in detail.

Commitment Scheme

First of all, commitment schemes are not specific to the PlonK protocol. They are a widely used cryptographic primitive. These schemes allow the prover (or in this context the committer) to commit to a piece of information while keeping it hidden from the verifier. The property that ties the committer to a specific piece of information is called binding. The second important property is hiding, which means that the prover cannot extract the committed information from the commitment. To use a metaphor, imagine that the committer locks his precious information into a container and gives it to the verifier. After this point, the committer does not have access to the committed information and thus cannot change it anymore. Moreover, since the box is locked, the verifier cannot reveal the information on his own. However, he can get access to the information by requesting the committer to unlock the box.

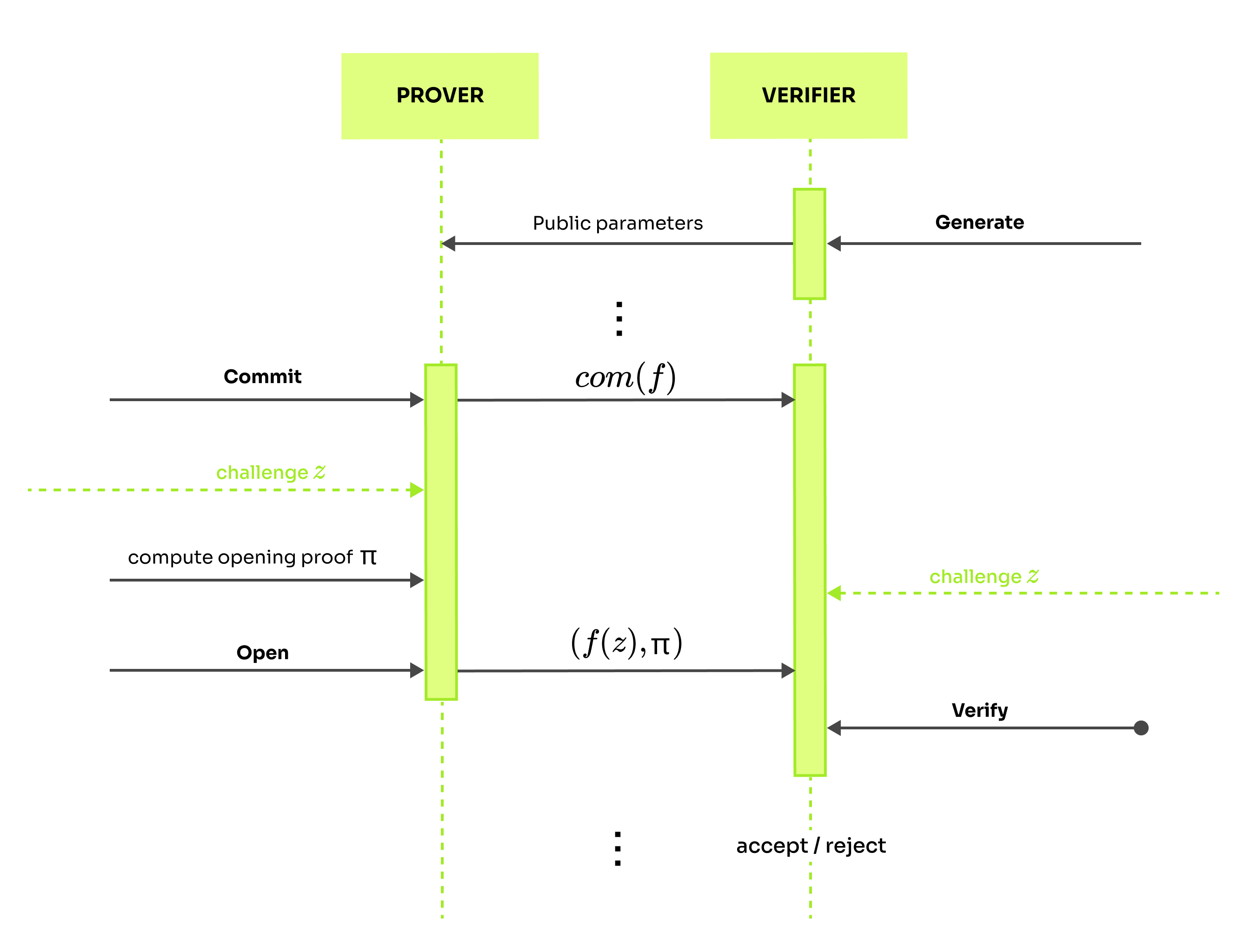
In the context of PlonK, we will be talking about polynomial commitment schemes (PCS). The secret information that the committer has is a description of a polynomial $f(x)$ with some degree bound (maximum degree) $d$ . To have a knowledge of a polynomial means to know its coefficients. The point of a PCS is to be able to commit to a polynomial and then prove its evaluation on an arbitrary point without giving away the coefficients. Understand it as a tool by which the verifier can reliably check the evaluation of a specific polynomial. So, PCS is not related to arguing that the prover has the correct polynomial. Instead, it is used to ensure that the answers provided by the prover are correct evaluations of the committed polynomial at a specific point. A standard non-interactive polynomial commitment scheme should have these procedures:

$\mathsf{Generate}$ : generate public parameters
$\mathsf{Commit}$ : calculate the commitment $C$ to $f(x)$ - make the prover "stick to" $f(x)$
$\mathsf{Open}$ : given a challenge $z$ the prover computes $v = f(z)$ and returns the tuple $(v, \pi)$ where $\pi$ is proof of the claim $v = f(z)$
$\mathsf{Verify}$ : given $(C, z, v, \pi)$ the verifier is checks $f(z) = v$ and outputs accept or reject

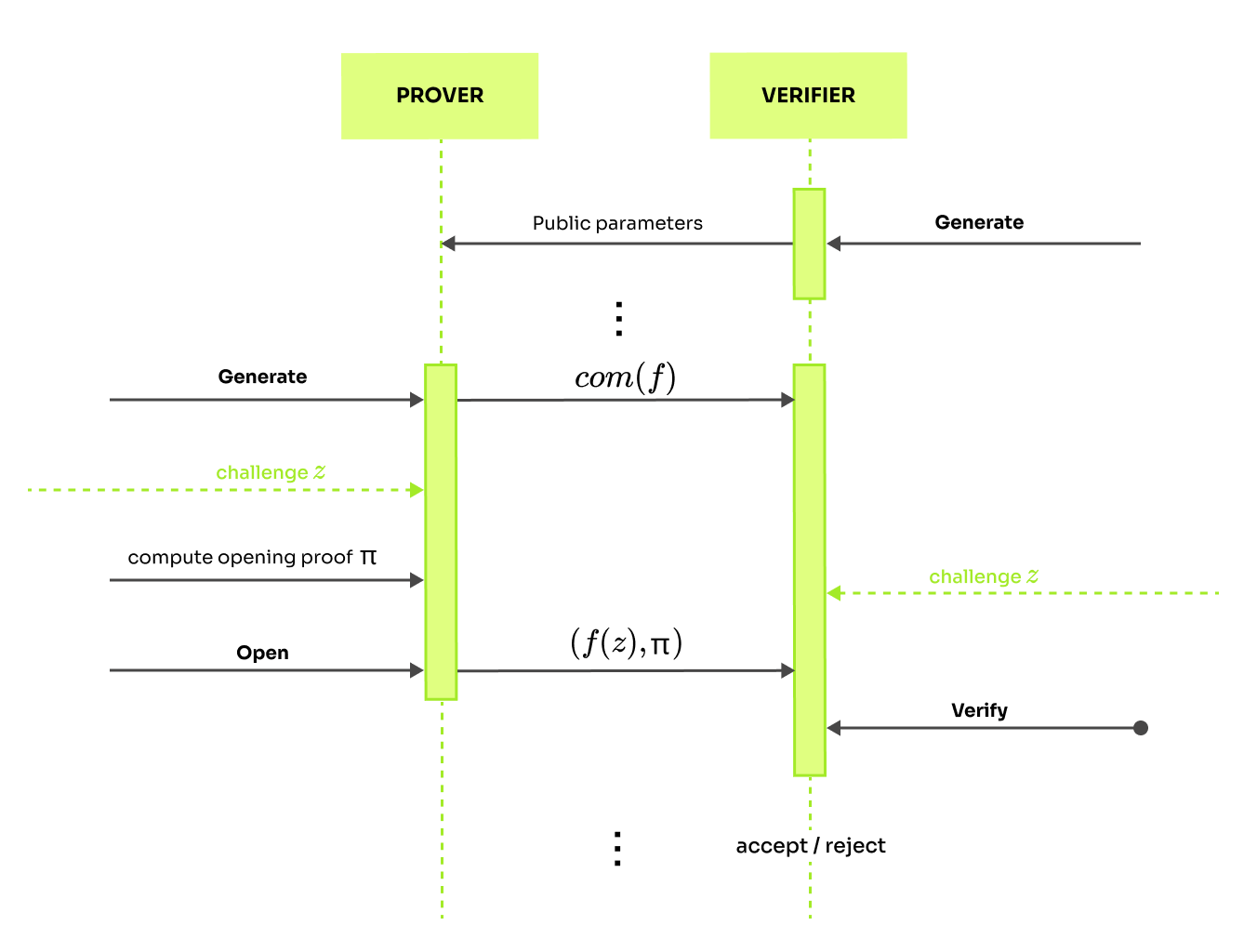
Simplified protocol of polynomial commitment scheme

For now, we will be somewhat secretive about the challenge $z$ and take it as given. Later, we will describe who provides the challenge. The motivation behind PCS is that the prover remains bound to the committed polynomial $f(x)$ and cannot choose it depending on the query $z$ he gets. This is formalized by the binding property.

KZG commitment scheme

There are numerous approaches to designing polynomial commitment schemes. We are specifically interested in KZG commitments since that is the one that was used in the PlonK paper. The nice thing about KZG is that commitment and opening consist of a constant number of elements. A disadvantage is that KZG has a trusted setup. Very informally, a trusted setup means that an enemy cannot discover a key that was used to generate the public parameters.

The following part is going to get a bit more technical, so if you do not know what elliptic curves are, we highly suggest reading Math Toolkit for KZG first. Let's summarize a list of all the public "ingredients" needed for KZG:

$(\mathbb{G}_1, \mathbb{G}_2, \mathbb{G}_t)$ : pairing friendly groups of points on an elliptic curve over a finite field $\mathbb{F}_p$ where $\mathbb{G}_t$ is the target group
$e$ : pairing $\mathbb{G}_1 \times \mathbb{G}_2 \rightarrow \mathbb{G}_t$
$G_1, G_2$ : generators of the groups $\mathbb{G}_1, \mathbb{G}_2$
$d$ : upper bound on the degree of committed polynomial
$SRS$ : public parameter - structured reference string

The last item on the list is the public parameter created by the $\mathsf{Generate}$ procedure. The $SRS$ is necessary for anyone who wants to make a commitment to a polynomial. In essence it is just a collection of points: $[{G_1, G_1^{\tau}, G_1^{\tau^2}, \ldots, G_1^{\tau^{d}}, G_2, G_2^{\tau}}]$ where $\tau \in \mathbb{F}_p$ is unformly randomly selected secret key used to generate the $SRS$ . The important thing is that the committer (prover) must not discover $\tau$ because that would allow him to forge openings and invalidate the protocol. That is why it is good practice to delete $\tau$ right after the $\mathsf{Generate}$ procedure and forget about it forever. Notice that some information about $\tau$ is known by everybody because it is contained in $SRS$ . However, the value is encoded as an elliptic curve point, which means it is hard to extract it due to the discrete logarithm problem on the elliptic curves. The $SRS$ can be reused to prove evaluations of an arbitrary polynomial that satisfies the degree bound $d$ . So, it is said that the KZG has a one-time trusted setup.

Evaluation check

The whole scheme relies on the following simple fact. For any univariate polynomial $f(x)$ of degree $d$ the assertion $f(z) = v$ is equivalent to checking if there exists polynomial $w(x)$ of degree smaller than $d$ such that: $w(x) = \frac{f(x)-v}{x-z}$

What is the intuition behind this check? (optional section)

We have a polynomial $f(x)$ , and we know that $f(z) = v$ . Using $f(x)$ we can construct $\tilde{f}(x) = f(x) - v$ which is 0 at $z$ . If $\tilde{f}(z) = 0$ then $z$ is the root of $\tilde{f}(x)$ so $\tilde{f}(x)$ could be also written as $\tilde{f}(x) = (x-z)w(x)$ . Now we do a bit of reordering: $\tilde{f}(x) = (x-z)w(x)$ $w(x) = \frac{\tilde{f}(x) }{x-z}$ $w(x) = \frac{f(x) - v}{x-z}$ Just like that, we can change from checking equality to checking divisibility.

It might look intimidating, but this is just an observation that it is possible to effectively transform an evaluation check into this divisibility check and vice versa. As discussed in the section about comparing polynomials, the equality of these expressions can be verified with high confidence just by evaluation at a single randomly chosen point.

Now, we can finally proceed with the description of KZG procedures. The scheme is sketched below, which might help you understand it better. If looking at the code works better for you, make sure to look at our implementation of KZG.

Generate

setup procedure

The value $\tau \in \mathbb{F}_p$ is chosen uniformly at random and $SRS$ is generated by exponentiation of the group generators $G_1, G_2$ . As discussed above the prover cannot discover the key $\tau$ . So the setup procedure cannot be done by the prover.

Commit

commit procedure

The prover has some secret polynomial $f(x)$ of degree at most $d$ . To commit to $f(x)$ , the prover sends commitment $C$ which he claims is equal to $G_1^{f(\tau)}$ . This means that commitment is a group element, which is just a point on the curve.

It might feel sneaky that the prover is asked to compute the evaluation $f(\tau)$ even though we explicitly said that the prover could not have access to $tau$ , so how is the evaluation calculated? Now, it will finally make sense why we need the $SRS$ . As described in the previous post polynomial evaluation of $f(x) = c_0 + c_1x + c_2x^2 + \ldots + c_dx^d$ in the exponent of the group generator can be calculated as: $G_1^{f(x)} = \prod_{i=0}^d (G^{x^i})^{c_i}$

We know how to compute commitment $G_1^{f(x)}$ for general $x$ , so now we just plug in $\tau$ as: $\prod_{i=0}^d (G_1^{\tau^i})^{c_i}$ . Note that $SRS$ contains all needed $G_1^{\tau^i}$ , which means that the prover does not (and in fact cannot) know $\tau$ to evaluate $G_1^{f(\tau)}$ . So, the committer gives an evaluation of polynomial $f$ on point $\tau$ (encoded as a group element) without knowing the actual point. What a cool trick, right?

To sum up, we took the prover's secret polynomial $f(x)$ and showed how to transform it into a group element by putting it into exponent $G_1^{f(x)}$ . Rewriting it like this allows us to use the SRS and evaluate $G_1^{f(\tau)}$ without knowing $\tau$ .

Open

open procedure

Given the query $z$ the prover opens the polynomial $f(x)$ at that point $v = f(z)$ , nothing complicated. Then, the committer needs to compute the witness: $w(x) = \frac{f(x)-v}{x-z}$ There is nothing special about that, the prover just needs to perform polynomial division. Showing the existence of is the same as verifying $f(z) = v$ . Therefore the polynomial $w(x)$ is the proof that $f(z) = v$ . Then the prover calculates $W = G_1^{w(\tau)}$ which is also possible to compute without knowledge of $\tau$ using the same approach as in the $\mathsf{Commit}$ procedure. Finally, the prover outputs the tuple $(v, W)$ .

Verify

verify procedure

Here might be a good place to revise that the polynomial commitment scheme is used to ensure polynomials are evaluated correctly. If the verification procedure succeeds, the verifier is convinced that the evaluation at the point $z$ on the committed polynomial is supposed to be $v$ . As we have seen above, this could be achieved by showing the existence of $w(x)$ . Without the fancy group pairings, the check is just: $w(\tau) \stackrel{?}{=} \frac{f(\tau)-v}{\tau-z}$ $f(\tau) - v \stackrel{?}{=} w(\tau){\tau-z}$

The prover does not know $\tau$ but can send $f(\tau), w(\tau)$ as elliptic curve points $C = G_1^{f(\tau)}, W = G_1^{w(\tau)}$ . The check changes to: $e(C G_1^{-v}, G_2) \stackrel{?}{=} e(W, G_2^{\tau}G_2^{-z})$

The verifier knows only $(C, z, v, W)$ and the public parameter SRS. Let's describe the expression from the left side. The verifier has the commitment $C$ which was sent by the committer. He is was given $v$ and needs to calculate $G_1^{-v}$ and $G_2$ is part of the $SRS$ .

On the right side, the verifier got the witness $W$ and $G_2^{\tau}$ is part of $SRS$ . He has the value $z$ and can calculate $G_2^{-z}$ , because G_2^ is part of the $SRS$ . The thing to notice is that the verifier would not be able to calculate $G^{w(\tau)(\tau - z)}$ without the pairings. Remember that $G^{w(\tau)}G^{\tau - z}$ would just give $G^{w(\tau) + \tau - z}$ , but the pairing property $(G_1^a, G_2^b) = G_t^{ab}$ makes it possible to calculate this operation.

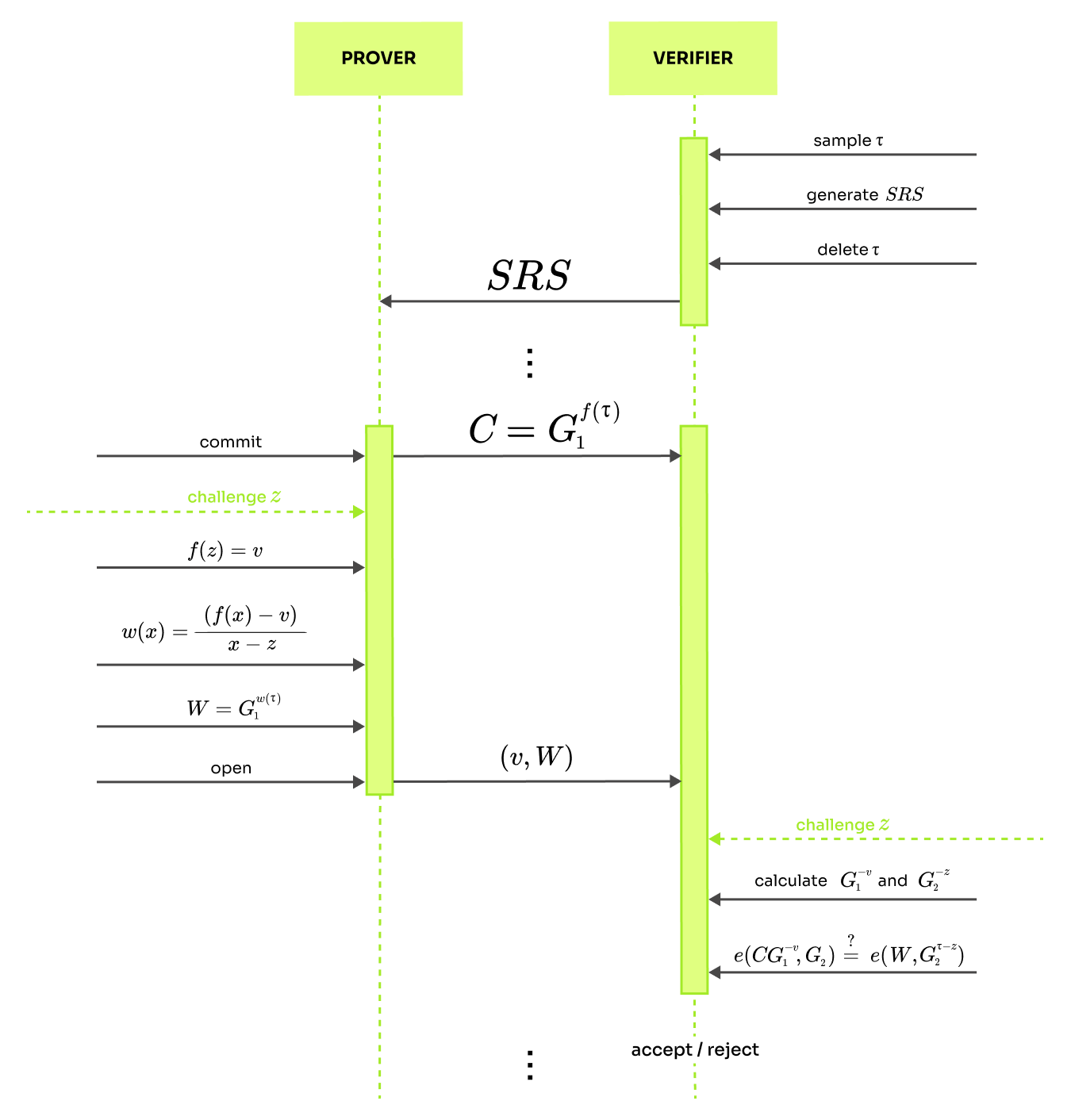
Even though the SRS string is big, notice that the verifier only needs to know $G_1, G_1^\tau, G_2, G_2^\tau$ , and the rest of $SRS$ is not needed. Another important thing is that the verifier discovers the evaluation $v = f(z)$ , which makes this not zero-knowledge. We will show how to fix this before giving the first commitment in Round 1 of the prover algorithm.

There are also more advanced flavors of KZG, where it is possible to batch: evaluations of a single polynomial at multiple points, evaluations of multiple polynomials at single points, or evaluations of multiple polynomials at multiple points. These are much more effective than running the commitment scheme for each separately.

One more important thing is that the calculation of the commitment can be generalized by the term multi-scalar multiplication (MSM), which is simply multiplication the elements of the $SRS$ by the coefficient of the committed polynomial. And MSM is a major bottle-neck of the $PlonK$ protocol and based on the Ingonyama can take up to $85-90$ % of prover time in $PlonK$ .

We will continue with the post about the setup algorithm for the $PlonK$ protocol, which produces preprocessed input for both the prover and the verifier.

List of the PlonK blog posts:

If you have any suggestions or improvements to this blog, send an e-mail to contact@maya-zk.com

PlonK Deconstructed 4: Polynomial Commitment Scheme