Round 4

The fourth round has little going on. The prover must compute openings to evaluate already committed polynomials. But there is a neat trick to make this more effective.

Round overview:

1. Compute evaluation challenge $\mathfrak{z} = \mathcal{H}(transcript)$

2. Compute and output opening evaluations $\bar{a}, \bar{b}, \bar{c}, \bar{z_\omega}$, $\bar{S}_{\sigma_1}$, $\bar{S}_{\sigma_2}$

Linearization trick (Maller optimization)

Say that the prover wants to show that $f_1(x)f_2(x) - f_3(x) = 0$ over the domain $H$. We will denote terms with horizontal line as openings $\bar{f}_1 = f_1(\mathfrak{z}), \bar{f}_2 = f_2(\mathfrak{z}), \bar{f}_3 = f_3(\mathfrak{z})$.

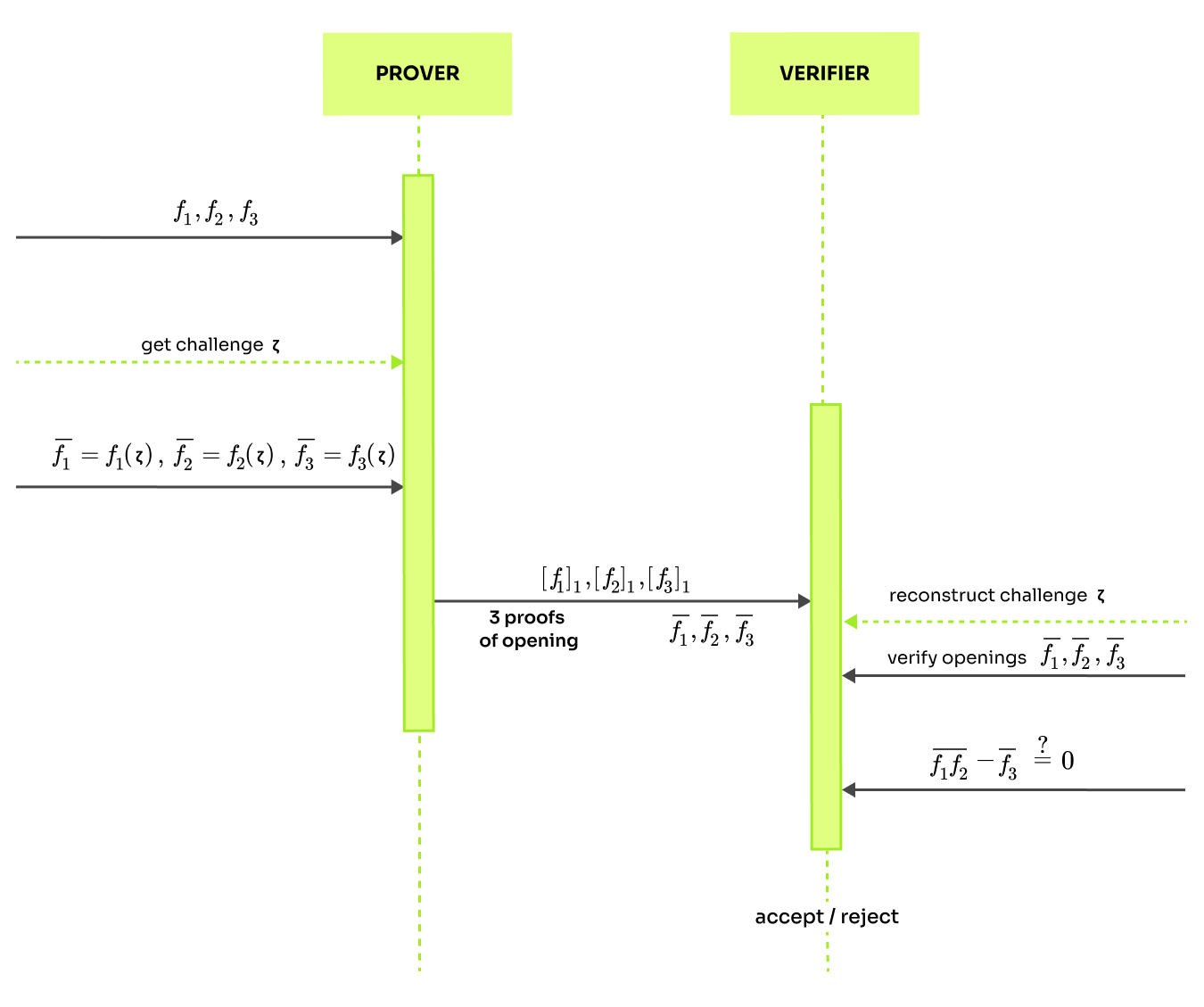
The standard way of proving this is to send 3 commitments and 3 polynomial openings at a randomly picked challenge $\mathfrak{z}$ and let the verifier check $\bar{f}_1\bar{f}_2 - \bar{f}_3 \stackrel{?}{=} 0$. Using the polynomial commitment scheme, the verifier can check if the openings are correct evaluations of the committed polynomials and as mentioned in math toolkit, it is sufficient to compare the polynomials at a single randomly picked point. In the interactive protocol, the verifier picks the challenge. In non-interactive case the challenge is picked by a random oracle after the prover commits to the polynomials.

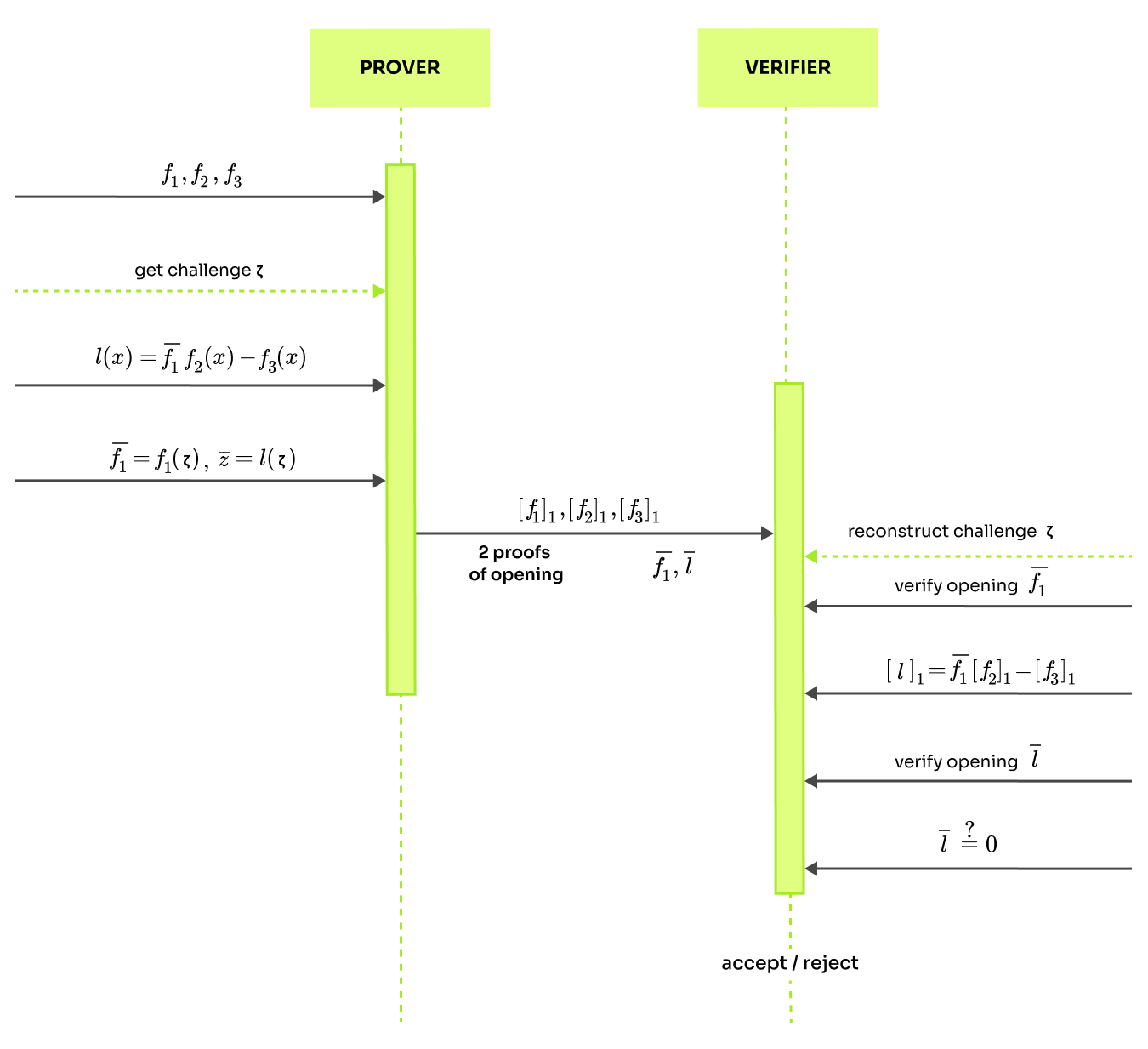
There is a better approach where the prover sends 3 commitments but just two 2 openings. This minimizes both the communication load and the proof size. The trick is in constructing a linearization polynomial: $l(x) = \bar{f}_1 f_2(x) - f_3(x)$. As before the prover needs to send commitments $[f_1]_1, [f_2]_1, [f_3]_1$, but only 2 openings $\bar{f}_1 = f_1(\mathfrak{z})$ and $\bar{l} = \bar{f}_1 f_2(\mathfrak{z}) - f_3(\mathfrak{z})$ and two proofs of opening (from polynomial commitment scheme).

The prover does not send commitment linearization polynomial $l(x)$, because the verifier can calculate $[l]_1$ on his own. Revise commitments are defined as $[f]_1 = G_1^{f(\tau)}$ elements of a group defined by points on an elliptic curve over a finite field $\mathbb{F}_p$ as explained in the KZG post. In the group, only one operation is defined between the group elements. This means that we can add commitments but not multiply them. However, it is possible to multiply a group element by a constant (in this case $\bar{f}_1$) so we can calculate $[l]_1 = \bar{f}_1[f_2]_1 - [f_3]_1$. This means that the linearization polynomial cannot contain polynomial multiplication, otherwise the verifier would not be able to calculate the commitment $[l]_1$.

So, if the verifier can reconstruct commitment to the linearization polynomial $[l]_1$, he is also able to check that the openings $\bar{l}, \bar{f}_1$ is a correct evaluation thanks to the 2 proof of opening he recieves from the prover. Since the linearization polynomial is constructed as $l(x) = \bar{f}_1f_2(x) - f_3(x)$ it means checking $\bar{l} \stackrel{?}{=} 0$ is equivalent to checking $\bar{f}_1\bar{f}_2 - \bar{f}_3 \stackrel{?}{=} 0$. The whole linearization trick is described more formally on page 18 of the PlonK paper.

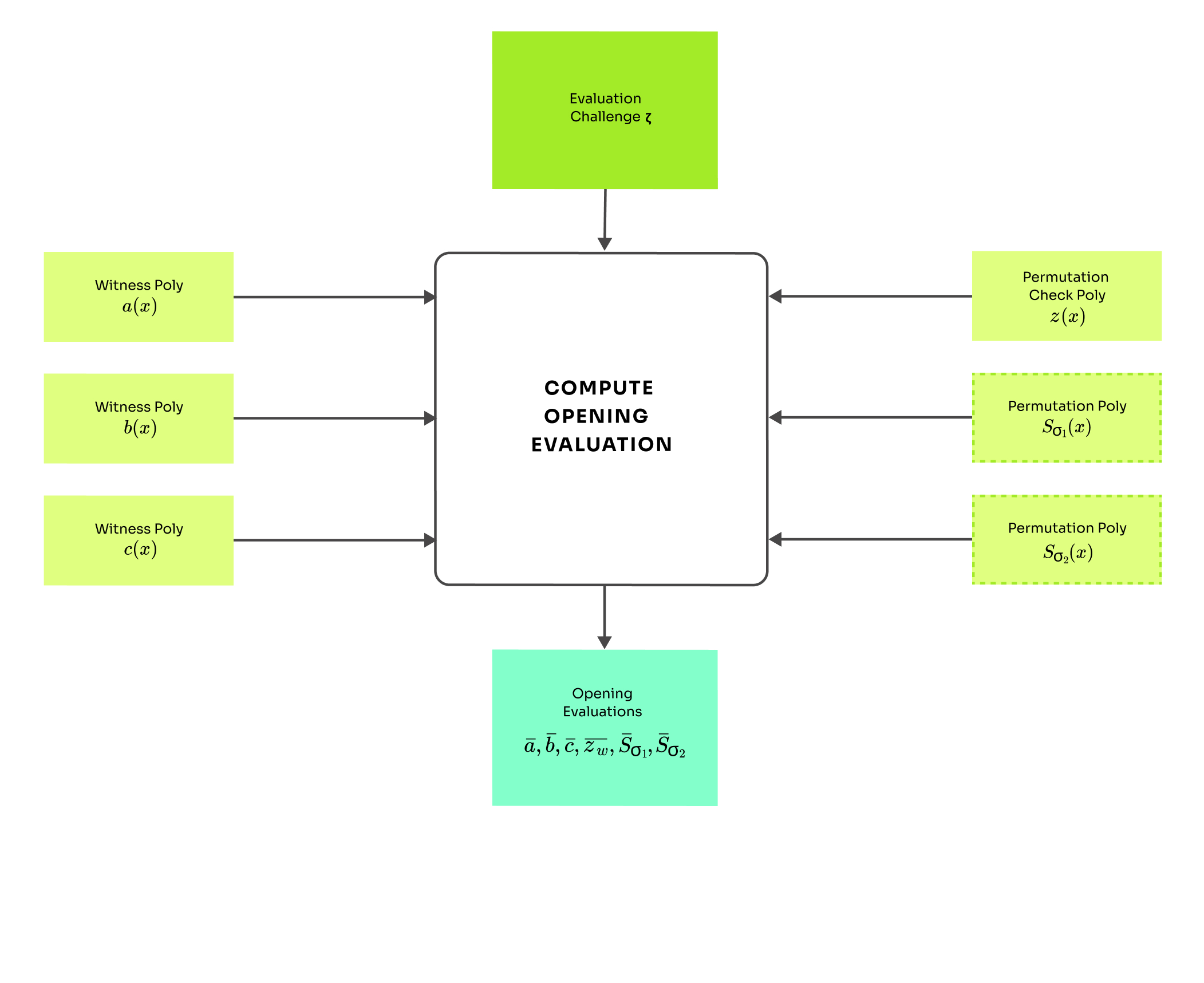
Polynomial openings

In this round, the prover does not construct any new polynomial and calculates just the opening at a challenge $\mathfrak{z}$ given by a random oracle. The non-interactive challenge generation is briefly explained in the round 1. The openings are calculated as: $\bar{a} = a(\mathfrak{z}), \bar{b} = b(\mathfrak{z}), \bar{c} = c(\mathfrak{z})$ $\bar{z}_\omega = z(\omega\mathfrak{z})$ $\bar{S}_{\sigma_1}$ $= S*{\sigma_1}(\mathfrak{z}),$ \bar{S},[object Object],2} $= S*{\sigma_2}(\mathfrak{z}),$

There are two things to notice about this. The prover sends evaluations $\bar{S}_{\sigma_1}$ $\bar{S}_{\sigma_2}$ but not $\bar{S}_{\sigma_3}$ and evaluation to the permutation polynomial is at $z(\mathfrak{z}\omega)$ instead of $z(\mathfrak{z})$. If you would like to know why, continue to the final round of the PlonK prover algorithm.

List of the PlonK blog posts:

• 1: Overview
• 2: Arithmetization
• 3: Math Preliminaries
• 4: KZG
• 5: Setup
• 6: Round 1
• 7: Round 2
• 8: Round 3
• 9: Round 4
• 10: Round 5
• 11: Verification

If you have any suggestions or improvements to this blog, send an e-mail to contact@maya-zk.com