Round 1

Finally, we can start with the first round of the prover algorithm where the prover computes wire polynomials and commits to them. But before that, we need to return to KZG and solve some of the problems we left unanswered. Specifically, we will show who generates evaluation challenges and how to hide the polynomial evaluations to get a zero-knowledge protocol.

Round overview:

Generate random blinding scalars $(b_1, ... ,b_9) \in \mathbb{F}_p$
Compute wire polynomials $a(x), b(x), c(x)$
Compute and output commitments $[a]_1, [b]_1, [c]_1 \in \mathbb{G}_1$

Challenges

When describing KZG, we said the challenge is "somehow" given. In the interactive case, this value could be given by the verifier, but we aim for a non-interactive protocol. Transforming an interactive protocol to a non-interactive might be done by the Fiat-Shamir heuristic, which suggests that the prover computes all of the challenges by himself using a random oracle. This oracle could be a cryptographic hash function $\mathcal{H}$ which takes variable-length input and gives fixed-length output. There is a formal definition of how this secure hash function should look, but we will not go into the details. The important properties are:

the oracle is deterministic - it always returns the same results if given the same input values
generated answers "look random" - outputs from the oracle should be indistinguishable from randomly generated sequences

When the prover needs to get a challenge, he will query the oracle $\mathcal{H}$ with some input. In the case of PlonK, the input to $\mathcal{H}$ will be the protocol transcript. Think of it as a summary of the protocol composed of:

the common preprocessed input described in the previous post
public input to the circuit
polynomial commitments and openings computed by the prover so far

The random oracle is also accessible by the verifier. Since it is deterministic and the transcript is public, the verifier can reconstruct the challenges in the verification phase. The main idea is simple, but this heuristic has some security assumptions one should be aware of. Possible vulnerabilities of incorrect implementations are mentioned in Weak Fiat-Shamir Attacks on Modern Proof Systems.

How does the verifier know that the prover did not cheat in picking the challenge? (optional section)

Based on the protocol, the prover queries the random oracle to obtain challenges. But what is stopping him from picking a suitable challenge by himself? The verification phase of KZG essentially checks that: $w(\tau) \stackrel{?}{=} \frac{f(\tau) - v}{\tau - z}$

However, if the prover tries to forge the proof and calculates the witness $w(\tau)$ and evaluation $v = f(z')$ using $z'$ that was not determined by the random oracle we get: $\frac{f(\tau) - f(z')}{\tau - z'} \stackrel{?}{=} \frac{f(\tau) - f(z')}{\tau - z}$

The values $\tau, z$ are fixed because $\tau$ is determined by the generation of SRS and $z$ by the random oracle. That means we are checking the equality of two different polynomials evaluated at $z'$ . From the post about math perliminaries we know that this check succeeds only with negligible probability. As result is it not possible to cheat the protocol because the verifier can retrieve the challenge $z$ from the random oracle check the validity of the polynomial opening.

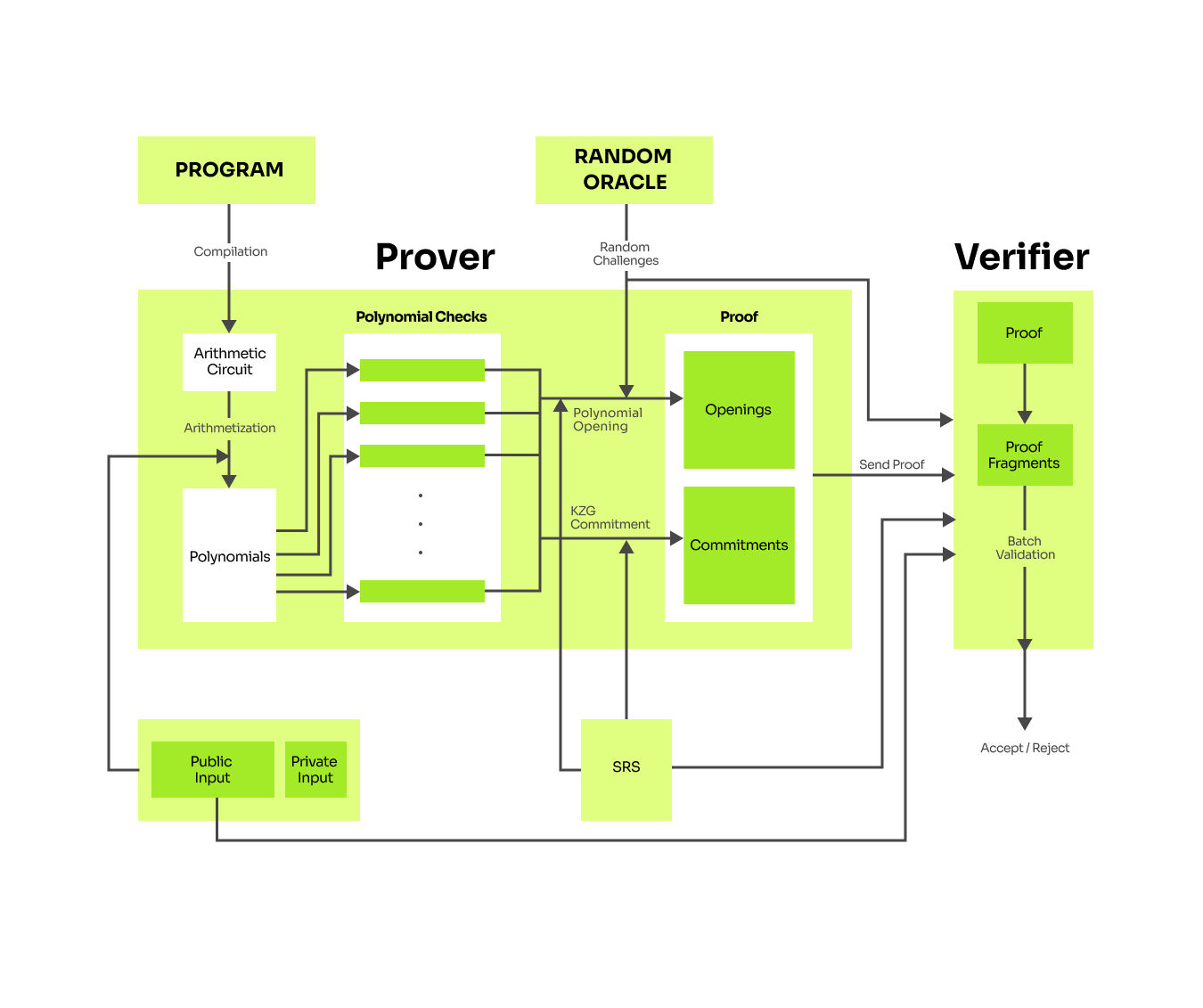
PlonK diagram revisited

With all that we have explained, we can reiterate the diagram of the PlonK protocol and be more detailed. In each round of the prover algorithm, we will create polynomials from the ingredients we've already computed. Finally, the prover sends the proof $\pi$ , composed of polynomial commitments and polynomial evaluations at a challenge given by the random oracle. The verifier reconstructs the transcript to calculate the challenges. Thanks to the polynomial commitment scheme he can verify the validity of openings and finally perform the check described in the verification algorithm.

Blinding

So far, we have discussed vanilla KZG polynomial commitment scheme that is not zero-knowledge. Opening a committed polynomial at challenge a point naturally reveals information about the polynomial. We are aiming to make the protocol zero-knowledge, so absolutely no information could leak. We will alter KZG in a way that the prover can convince the verifier about the validity of the evaluation, but the verifier does not discover the actual evaluation. To achieve this, we will use blinding scalars (randomly sampled numbers with a fancy name) and a vanishing polynomial (a polynomial with a fancy name).

Vanishing polynomial

The vanishing polynomial is a polynomial with roots as all elements of the domain $H$ , meaning $\forall x \in H: Z_H(x) = 0$ . Therefore the polynomial could be factored as $Z_H(x) = (x - 1)(x - \omega)(x - \omega^2), ..., (x - \omega^{n-1})$ . We set the evaluation domain $H$ to be generated by the primitive $n$ -th roots of unity $\omega$ . Given this fact, the vanishing polynomial could be compactly written as $x^n-1$ as showed in the previous post.

Blinding of the committed polynomial is achieved by introducing randomness. PlonK achieves this by mangling the former polynomial $f(x)$ as follows: $f'(x) = Z_H(x) \times \text{some expression} + f(x)$

The polynomials $f(x), f'(x)$ agree on all points of domain $H$ , because $Z_H(x)$ is 0 over the whole domain $H$ . So, we have randomized the polynomial, but made sure that the evaluation on $H$ remains the same.

Blinding scalars

Consider that a polynomial $f(x)$ is opened at challenge points $(z_1, z_2, ... z_{k})$ chosen by the oracle. The PlonK paper protocol suggests altering the committed polynomial with random blinding scalars $(b_1, b_2, \ldots, b_{k+1}) \in \mathbb{F}_p$ as: $f'(x) = (b_1 + b_2x + b_3x^2 ... + b_{k+1}x^{k})Z_H(X) + f(x)$

The number of blinding scalars should be at least the number of openings of $f(x)$ plus 1. Now, does $f'(x)$ reveal some information about $f(x)$ ? Well, it does because for $\forall x \in H: f(x) = f'(x)$ . However, the challenges are chosen by the random oracle, which guarantees that they are chosen randomly. Since the size of the evaluation domain is small compared to the order of the field $\mathbb{F}_p$ , the probability of picking a random element of $H$ is $|H| / p$ , which is considered to be negligible.

If the chosen challenges are not from $H$ then the polynomial is blidned and it is hard to extract the original polynomial from the blinded one. The proof of why this masking guarantees zero knowledge was not initially included in the PlonK paper. If you are interested in proof, take a look at section 4.2 of the PlonKup protocol.

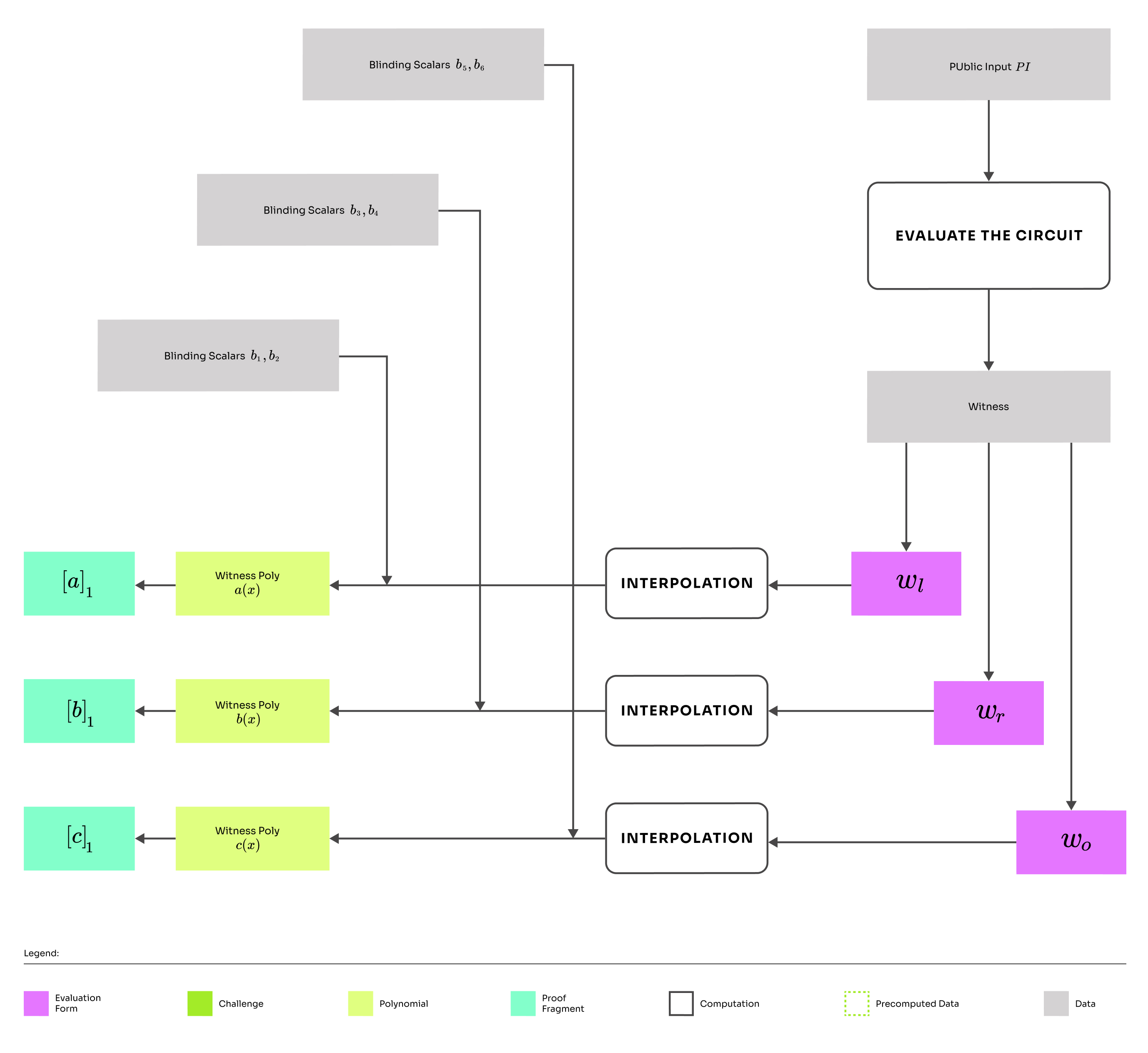
Computing wire polynomials

We will use the notation $[f]_1 = G_1^{f(\tau)}$ for commitments to polynomials. Commitments will be polynomials evaluated at the secret $\tau$ (using SRS) and encoded as a point of an elliptic curve.

Round 1 essentially binds the prover to the witness by constructing polynomials from the computational table and committing to them. The vectors $w_{l}, w_{r}, w_{o}$ introduced in arithmetization represent the colums of the computational table. We represent each column as a wire polynomial by applying Lagrange interpolation and adding randomization in the form of blinding scalars. The blinding scalars are uniformly randomly and independently sampled by the prover.

$a(x) = (b_1x + b_2)Z_H(x) + \sum_{i=0}^{n-1} w_{l_i} L_i(x)$ $b(x) = (b_3x + b_4)Z_H(x) + \sum_{i=0}^{n-1} w_{r_i} L_i(x)$ $c(x) = (b_5x + b_6)Z_H(x) + \sum_{i=0}^{n-1} w_{o_i} L_i(x)$

After constructing these polynomials, the prover constructs commitments $[a]_1, [b]_1, [c]_1$ as specified in KZG.

We will continue with round 2 of the prover algorithm and show how to ensure that the copy constraints of an arithmetic circuit hold.

List of the PlonK blog posts:

If you have any suggestions or improvements to this blog, send an e-mail to contact@maya-zk.com

PlonK Deconstructed 6: Round 1